Câu hỏi:
26/12/2022 3,810
Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích →AN qua các vectơ →a và →b ta được biểu thức là:
Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích →AN qua các vectơ →a và →b ta được biểu thức là:
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: B.
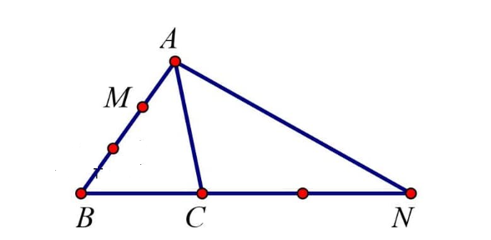
Theo đề bài: CN = 2BC nên →BN=3→BC
Ta có:
→AN=→AB+→BN=→AB+3→BC=→AB+3(→AC−→AB)=−2→AB+3→AC=−2→a+3→b.
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ →AG qua các vectơ →AB và →AC ta được →AG=ab→AB+cd→AC với ab và cd là các phân số tối giản. Khi đó ta có: ab+cd=?
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN và G là trọng tâm tam giác MNB. Phân tích vectơ →AG qua các vectơ →AB và →AC ta được →AG=ab→AB+cd→AC với ab và cd là các phân số tối giản. Khi đó ta có: ab+cd=?
Xem đáp án »
10/08/2022
28,996
Câu 2:
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. G là trọng tâm của tam giác ABC. Phân tích vectơ →MN qua các vectơ →GA và →GB.
Cho tam giác ABC, trên cạnh BC lấy M sao cho BM = 3CM, trên đoạn AM lấy N sao cho 2AN = 5MN. G là trọng tâm của tam giác ABC. Phân tích vectơ →MN qua các vectơ →GA và →GB.
Xem đáp án »
10/08/2022
12,316
Câu 3:
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2→IC=3→BI. Phân tích vectơ →AI theo hai vectơ →AB và →AC.
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2→IC=3→BI. Phân tích vectơ →AI theo hai vectơ →AB và →AC.
Xem đáp án »
10/08/2022
2,020
Câu 4:
Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ →AB theo hai vectơ →AK=→u và →BM=→v ta được biểu thức là:
Cho AK và BM là hai trung tuyến của tam giác ABC. Phân tích vectơ →AB theo hai vectơ →AK=→u và →BM=→v ta được biểu thức là:
Xem đáp án »
10/08/2022
1,802
Câu 5:
Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ →GC qua các vectơ →GA và →GB.
Cho tam giác ABC, G là trọng tâm của tam giác ABC. Phân tích vectơ →GC qua các vectơ →GA và →GB.
Xem đáp án »
10/08/2022
568
Câu 6:
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ →AN qua các vectơ →AB và →AC.
Cho hình bình hành ABCD. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh AB và CD sao cho AB = 3AM, CD = 2CN. Biểu diễn vectơ →AN qua các vectơ →AB và →AC.
Xem đáp án »
10/08/2022
560
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
-
15 câu Trắc nghiệm Toán 10 Kết nối tri thức Quy tắc đếm có đáp án
-
10 Bài tập Các bài toán thực tế ứng dụng nhị thức Newton (có lời giải)
-
10 Bài tập Viết phương trình cạnh, đường cao, trung tuyến, phân giác của tam giác (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận