Câu hỏi:
11/07/2024 868
Cho nửa đường tròn (O) đường kính AB = 2R. Điểm C (khác A) bất kì nằm trên nửa đường tròn sao cho AC < CB. Điểm D thuộc cung nhỏ BC sao cho COD = 90o. Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD.
a) Chứng minh CEDF là tứ giác nội tiếp.
Cho nửa đường tròn (O) đường kính AB = 2R. Điểm C (khác A) bất kì nằm trên nửa đường tròn sao cho AC < CB. Điểm D thuộc cung nhỏ BC sao cho COD = 90o. Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD.
a) Chứng minh CEDF là tứ giác nội tiếp.
Sale Tết giảm 50% 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 49k/cuốn).
Quảng cáo
Trả lời:
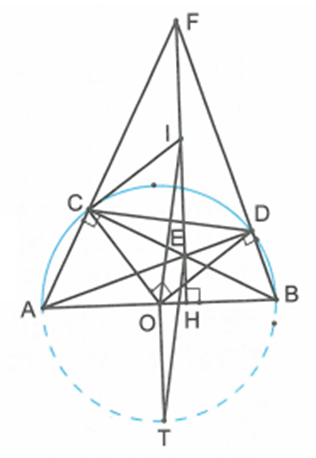
Ta có ACB = ADB = 90o (góc nội tiếp chắn nửa đường tròn)
=> FCE = FDE = 90o.
Tứ giác CEDF có FCE + FDE = 180o => CEDF là tứ giác nội tiếp.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC ( E khác B và C ), AE cắt CD tại F. Chứng minh BEFI là tứ giác nội tiếp đường tròn.
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC ( E khác B và C ), AE cắt CD tại F. Chứng minh BEFI là tứ giác nội tiếp đường tròn.
Câu 2:
Cho tam giác ABC và đường cao AH. Gọi M, N lần lượt là trung điểm của AB, AC. Đường tròn ngoại tiếp tam giác BHM cắt đường tròn ngoại tiếp tam giác CNH tại E. Chứng minh AMEN là tứ giác nội tiếp và HE đi qua trung điểm của MN.
Cho tam giác ABC và đường cao AH. Gọi M, N lần lượt là trung điểm của AB, AC. Đường tròn ngoại tiếp tam giác BHM cắt đường tròn ngoại tiếp tam giác CNH tại E. Chứng minh AMEN là tứ giác nội tiếp và HE đi qua trung điểm của MN.
Câu 3:
c) Gọi I là trung điểm của EF. Chứng minh IC là tiếp tuyến của (O).
c) Gọi I là trung điểm của EF. Chứng minh IC là tiếp tuyến của (O).
Câu 5:
d) Hỏi khi C thay đổi thỏa mãn điều kiện bài toán, E thuộc đường tròn cố định nào?
Bình luận
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 02
-
23 câu Trắc nghiệm Toán 9 Bài 1: Căn thức bậc hai có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 06
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 03
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 05
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải

về câu hỏi!