Cho ΔABC có đường cao AH, biết AB=30cm, BH=18cm; AC=40cm Tính độ dài AH và chứng minh: ΔABH ”
Quảng cáo
Trả lời:
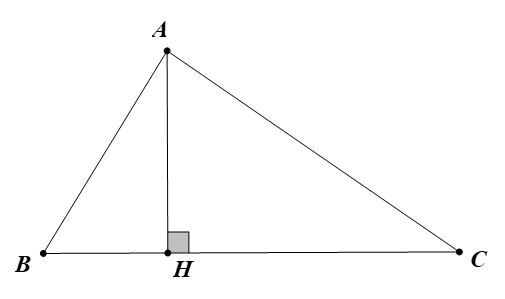
a) Vì vuông tại H, theo định lý Pitago ta có:
Vì vuông tại H, theo định lý Pitago ta có:
Ta lại có:
Xét và có:
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

Vẽ Xét ABH và ACE có chung .
Suy ra
(1)
Xét và có (so le trong)
Suy ra (2)
Cộng vế theo vế (1) và (2) ta được:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.