Câu hỏi:
22/02/2023 338Cho mặt cầu S (O;4) cố định. Hình nón (N) gọi là nội tiếp mặt cầu S(O;4) nếu hình nón (N) có đường tròn đáy và đỉnh thuộc mặt cầu S( O;4). Tính bán kính đáy r của (N) để khối nón (N) có thể tích lớn nhất ?
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa... kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 70k).
Quảng cáo
Trả lời:
Chọn D
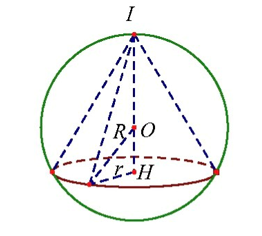
Gọi I là đỉnh và H là tâm đáy của hình nón (N) . Do IH⊥mp(H);OH⊥mp(H)
⇒I,O,H thẳng hàng.
Dễ thấy để (N) có thể tích lớn nhất thì chỉ cần O nằm giữa đoạn IH.
Gọi đường cao của hình nón là: h=IH=OI+OH=R+OH,R≤h≤2R.
Suy ra r2=R2−(h−R)2.
Thể tích khối nón là: V=13.πr2h=13.πh[R2−(h−R)2]=13.π(−h3+2Rh2)=f(h).
Ta có f', cho
Bảng biến thiên:
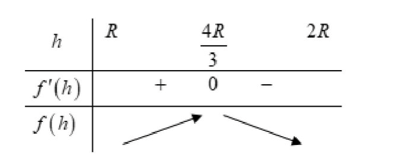
Vậy max khi
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian Oxyz, cho ba điểm và . Tìm tọa độ trực tâm H của tam giác ABC.
Câu 2:
Trong không gian Oxyz cho điểm . Tìm tọa độ N đối xứng với M qua trục Oy .
Câu 3:
Trong không gian Oxyz cho hai vectơ thoả mãn . Tính độ dài vectơ
Câu 4:
Một hình chữ nhật nội tiếp trong nửa đường tròn bán kính R= 6cm , biết một cạnh của hình chữ nhật nằm dọc theo đường kính của đường tròn mà hình chữ nhật đó nội tiếp. Tính diện tích lớn nhất của hình chữ nhật đó.
Câu 5:
Trong không gian Oxyz, cho điểm . Gọi M,N,P lần lượt là hình chiếu của A trên các trục và Oz. Tính diện tích S của tam giác MNP.
Câu 7:
Trong không gian Oxyz, cho mặt cầu . Khi đó (S) có tâm I và bán kính R lần lượt là
Bình luận
🔥 Đề thi HOT:
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
50 bài tập Nguyên hàm, tích phân và ứng dụng có lời giải
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
Đề minh họa THPT Quốc gia môn Toán năm 2023 có đáp án
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 3)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 5)

về câu hỏi!