Câu hỏi:
31/03/2023 7,621
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m∈[−20;20] để hàm số f(x)=3x4+4(1−2m2)x3+6(m−2m2)x2+12mx−1 nghịch biến trên khoảng (0;1)?
Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m∈[−20;20] để hàm số f(x)=3x4+4(1−2m2)x3+6(m−2m2)x2+12mx−1 nghịch biến trên khoảng (0;1)?
Đáp án chính xác
Câu hỏi trong đề:
(2023) Đề thi thử Toán THPT Chuyên Thái Bình (Lần 1) có đáp án !!
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
Ta có: f'(x)≤0,∀x∈(0;1)⇔12x3+12(1−2m2)x2+12(m−2m2)x+12m≤0,∀x∈(0;1)
⇔x2(x+1)−2m2x.(x+1)+m(x+1)≤0,∀x∈(0;1)⇔(x+1)(x2−2m2x+m)≤0,∀x∈(0;1)
Vì x∈(0;1)⇒x+1>0 nên yêu cầu bài toán ⇔x2−2m2x+m⏟g(x)≤0,∀x∈(0;1). (*)
Xét Δg(x)'=m4−m
TH1: Δg(x)'<0, do a=1>0⇒g(x)>0,∀x∈ℝ (không thỏa mãn).
TH2: Δg(x)'=0⇔[m=1m=0 (không thỏa mãn).
TH3: Δg(x)'>0⇔m4−m>0⇔[m>1m<0
Khi đó g(x)=0 có 2 nghiệm phân biệt (giả sử x1<x2).
Ta có bảng xét dấu của g(x) như sau:
![Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m thuộc [-20;20] để hàm số f(x) = 3x^4 + 4(1-m^2)x^3 + 6(m - 2m^2)x^2 + 12mx - 1 nghịch biến trên khoảng (0;1)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/03/blobid4-1680204155.png)
Theo yêu cầu bài toán ta có {g(0)≤0g(1)≤0⇔{m≤01−2m2+m≤0⇔{m≤0[m≥1m≤−12⇔m≤−12
Do {m∈ℤm∈[−20;20] nên ta nhận m∈{−20;−19;...;−1}. Vậy có tất cả 20 giá trị thỏa mãn.
Nhà sách VIETJACK:
Sách - 250+ Công thức giải nhanh môn Toán 12 Vietjack theo chương trình mới cho 2k7
Đã bán 1,3k
₫ 36.000
₫ 18.000
Combo - Sách 20 Bộ đề, Tổng ôn, sổ tay ôn thi 2025 môn Toán (3 quyển) - Mới nhất cho 2k7
Đã bán 386
₫ 110.000
₫ 55.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABC có đáy ABC là tam giác đều và SA vuông góc với đáy, AB = a. Khoảng cách từ C đến mặt phẳng (SAB) bằng
Cho hình chóp S.ABC có đáy ABC là tam giác đều và SA vuông góc với đáy, AB = a. Khoảng cách từ C đến mặt phẳng (SAB) bằng
Xem đáp án »
30/03/2023
34,901
Câu 2:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SA = a. Khoảng cách giữa hai đường thẳng SB và CD là
Xem đáp án »
31/03/2023
26,938
Câu 3:
Chọn ngẫu nhiên hai số trong 15 số nguyên dương đầu tiên. Xác suất chọn được hai số chẵn bằng
Chọn ngẫu nhiên hai số trong 15 số nguyên dương đầu tiên. Xác suất chọn được hai số chẵn bằng
Xem đáp án »
30/03/2023
21,281
Câu 4:
Cho khối chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, ^ABC=60°, cạnh bên SA vuông góc với đáy, mặt bên (SCD) tạo với đáy một góc 60o. Thể tích khối chóp S.ABCD bằng
Cho khối chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a, ^ABC=60°, cạnh bên SA vuông góc với đáy, mặt bên (SCD) tạo với đáy một góc 60o. Thể tích khối chóp S.ABCD bằng
Xem đáp án »
30/03/2023
18,556
Câu 5:
Cho hàm số có đồ thị là đường cong trong hình bên. Hàm số y = f(-x) nghịch biến trong khoảng nào dưới đây?
Cho hàm số có đồ thị là đường cong trong hình bên. Hàm số y = f(-x) nghịch biến trong khoảng nào dưới đây?
Xem đáp án »
30/03/2023
18,146
Câu 6:
Cho hàm số có đồ thị (C). Viết phương trình tiếp tuyến với (C) tại điểm A thuộc (C) có hoành độ bằng 1 .
Xem đáp án »
31/03/2023
17,352
Câu 7:
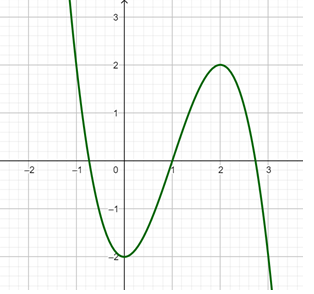
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
![Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Giá trị lớn nhất của hàm số g(x) = 2f(x) - 1 trên đoạn [-1;2] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/03/blobid6-1680192072.png)
Giá trị lớn nhất của hàm số g(x) = 2f(x) - 1 trên đoạn [-1;2] là
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Giá trị lớn nhất của hàm số g(x) = 2f(x) - 1 trên đoạn [-1;2] là
Xem đáp án »
30/03/2023
11,882
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
45 bài tập Xác suất có lời giải
-
50 bài tập Nguyên hàm, tích phân và ứng dụng có lời giải
-
50 bài tập Hình học không gian có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận