Câu hỏi:
13/07/2024 1,026
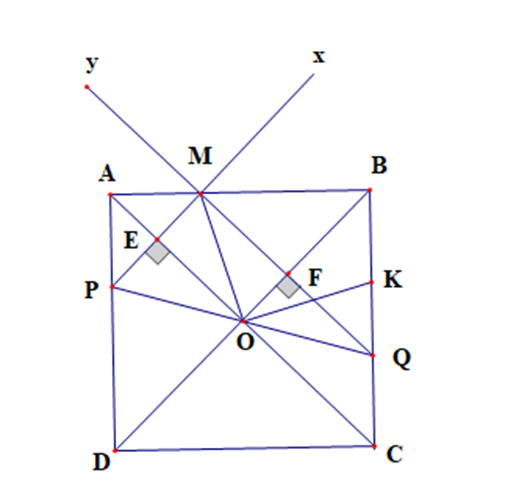
Cho hình vuông ABCD, gọi O là tâm của hình vuông. Một đường thẳng qua O cắt AD tại P, cắt BC tại Q.
a) Chứng minh AP = CQ
b) Kẻ Px vuông góc AC tại E (E thuộc AC). Kẻ Qy vuông góc BD tại F (F thuộc BD), Px và Qy cắt nhau tại M. Chứng minh OEMF là hình chữ nhật.
c) Chứng minh M thuộc cạnh AB
d) Lấy K thuộc BC sao cho CK = DP. Chứng minh ^MOK=90∘.
Cho hình vuông ABCD, gọi O là tâm của hình vuông. Một đường thẳng qua O cắt AD tại P, cắt BC tại Q.
a) Chứng minh AP = CQ
b) Kẻ Px vuông góc AC tại E (E thuộc AC). Kẻ Qy vuông góc BD tại F (F thuộc BD), Px và Qy cắt nhau tại M. Chứng minh OEMF là hình chữ nhật.
c) Chứng minh M thuộc cạnh AB
d) Lấy K thuộc BC sao cho CK = DP. Chứng minh ^MOK=90∘.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vì ABCD là hình vuông tâm O
Nên OA = OB = OC = OD, AB = BC = CD = DA, AD // BC
Suy ra ^DAC=^ACB (hai góc so le trong)
Xét tam giác AOP và tam gíc COQ có
^DAC=^ACB (chứng minh trên)
OA = OC (chứng minh trên)
^AOP=^COQ (hai góc đối đỉnh)
Do đó ΔAOP = ΔCOQ (g.c.g)
Suy ra AP = CQ (hai cạnh tương ứng)
b) Vì AB = AD nên tam giác ABD cân tại A
Mà AO là đường trung tuyến
Suy ra AO là đường cao
Hay AO ⊥ BD
Xét tứ giác OEMF có
^OEM=^EOF=^OFM=90∘
Suy ra OEMF là hình chữ nhật
c) Vì OEMF là hình chữ nhật
Nên ^FME=90∘
Hay tam giác PMQ vuông tại M
Mà MO là trung tuyến
Suy ra OM = OP = OQ
Do đó tam giác POM cân tại O
Lại có OE là đường cao nên OE là phân giác của ^POM
Suy ra ^POE=^EOM
Xét tam giác AOP và tam giác AOM có
AO là cạnh chung
^POE=^EOM (chứng minh trên)
OM = OP (chứng minh trên)
Suy ra △AOP = △AOM (c.g.c)
Do đó ^APO=^AMO (hai góc tương ứng)
Ta có OM = OQ
Do đó tam giác QOM cân tại O
Lại có OF là đường cao nên OF là phân giác của ^QOM
Suy ra ^QOF=^FOM
Xét tam giác BOQ và tam giác BOM có
BO là cạnh chung
^QOF=^FOM (chứng minh trên)
OM = OQ (chứng minh trên)
Suy ra △ BOQ = △BOM (c.g.c)
Do đó ^BQO=^BMO (hai góc tương ứng)
Vì AD // BC nên ^APO+^BQO=180∘
Mà ^BQO=^BMO, ^APO=^AMO
Suy ra ^AMO+^BMO=180∘
Hay ^AMB=180∘
Do đó A, M, B thẳng hàng
Vậy M thuộc cạnh AB
d) Ta có: AP = AD – DP, BK = BC – CK
Mà AD = BC, PD = CK
Suy ra AP = BK
Vì ABCD là hình vuông tâm O
Nên ^DAO=^OBC=45∘
Xét tam giác POA và tam giác KOB có
OA = OB
^DAO=^OBC (chứng minh trên)
PA = BK (chứng minh trên)
Suy ra △POA = △KOB (c.g.c)
Do đó ^POA=^KOB (hai góc tương ứng)
Mà ^POA=^AOM
Nên ^KOB=^AOM
Mặt khác ^AOM+^MOB=^AOB=90∘ (hai góc kề bù)
Suy ra ^BOK+^MOB=90∘
Hay ^MOK=90∘
Vậy ^MOK=90∘.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R):
a) y = f(x) = 3x+1x2+2(m−1)x+m2+3m+5
b) y = f(x) = √x2+2(m−1)x+m2+m−6
c) y = f(x) = 3x+5x2−2(m+3)x+m+9
Tìm m để các hàm số sau có tập xác định là R (hay luôn xác định trên R):
a) y = f(x) = 3x+1x2+2(m−1)x+m2+3m+5
b) y = f(x) = √x2+2(m−1)x+m2+m−6
c) y = f(x) = 3x+5x2−2(m+3)x+m+9
Xem đáp án »
13/07/2024
35,318
Câu 2:
Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:
→AB+→CD+→EF=→AD+→EB+→CF
Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:
→AB+→CD+→EF=→AD+→EB+→CF
Xem đáp án »
13/07/2024
17,086
Câu 3:
Cho tam giác ABC có AB = 2, BC = 4, CA = 3.
a) Tính →AB.→AC, rồi suy ra cosA
b) Gọi G là trọng tâm của △ABC. Tính →AG.→BC
c) Tính giá trị biểu thức S = →GA.→GB+→GB.→GC+→GC.→GA
d) Gọi AD là phân giác trong của góc BAC (D ∈ BC). Tính →AD theo →AB;→ACsuy ra AD.
Cho tam giác ABC có AB = 2, BC = 4, CA = 3.
a) Tính →AB.→AC, rồi suy ra cosA
b) Gọi G là trọng tâm của △ABC. Tính →AG.→BC
c) Tính giá trị biểu thức S = →GA.→GB+→GB.→GC+→GC.→GA
d) Gọi AD là phân giác trong của góc BAC (D ∈ BC). Tính →AD theo →AB;→ACsuy ra AD.
Xem đáp án »
13/07/2024
8,983
Câu 4:
Tỉ lệ phế phẩm của một nhà máy là 5%. Tìm xác xuất để trong 12 sản phẩm do nhà máy đó sản xuất ra có
a) 2 phế phẩm
b) không quá 2 phế phẩm.
Tỉ lệ phế phẩm của một nhà máy là 5%. Tìm xác xuất để trong 12 sản phẩm do nhà máy đó sản xuất ra có
a) 2 phế phẩm
b) không quá 2 phế phẩm.
Xem đáp án »
13/07/2024
7,182
Câu 5:
Một thiết bị gồm có 3 bộ phận. Trong khoảng thời gian T, việc các bộ phận đó bị hỏng là độc lập với nhau và với các xác suất tương ứng là: 0,1; 0,2; 0,3. Cả thiết bị sẽ bị hỏng nếu có ít nhất một bộ phận hư hỏng. Tìm xác suất thiết bị hoạt động tốt trong thời gian T đó.
Một thiết bị gồm có 3 bộ phận. Trong khoảng thời gian T, việc các bộ phận đó bị hỏng là độc lập với nhau và với các xác suất tương ứng là: 0,1; 0,2; 0,3. Cả thiết bị sẽ bị hỏng nếu có ít nhất một bộ phận hư hỏng. Tìm xác suất thiết bị hoạt động tốt trong thời gian T đó.
Xem đáp án »
13/07/2024
7,110
Câu 6:
Tìm tập xác định của hàm số sau:
a) y = 3x2 – 2x + 1
b) y = 3|x|+2x−2
c) y = √x−2+√3−x
d) y = 2x−1√4−3xx
e) y = √x+32−x
f) y = 2x+1x2−3x+2
g) y = x−1x2−1−3x
Tìm tập xác định của hàm số sau:
a) y = 3x2 – 2x + 1
b) y = 3|x|+2x−2
c) y = √x−2+√3−x
d) y = 2x−1√4−3xx
e) y = √x+32−x
f) y = 2x+1x2−3x+2
g) y = x−1x2−1−3x
Xem đáp án »
13/07/2024
5,856
Câu 7:
Cho tứ giác ABCD có AB = AD; CB = CD (ta gọi tứ ABCD trong trường hợp này là tứ giác có hình ảnh cánh diều)
a) Chứng minh AC là đường trung trực của BD
b) Tính góc B và góc D (biết ˆA=100∘,ˆC=60∘).
Cho tứ giác ABCD có AB = AD; CB = CD (ta gọi tứ ABCD trong trường hợp này là tứ giác có hình ảnh cánh diều)
a) Chứng minh AC là đường trung trực của BD
b) Tính góc B và góc D (biết ˆA=100∘,ˆC=60∘).
Xem đáp án »
13/07/2024
3,906
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận