Câu hỏi:
12/07/2024 20,898
Cho điểm M nằm ngoài đường tròn ( O; R ) sao cho OM = 2R. Từ M kẻ các tiếp tuyến MA, MB với đường tròn O (A, B là các tiếp điểm ). Kẻ đường kính AC của đường tròn (O). Gọi H là giao điểm của AB và OM.
a) Chứng minh 4 điểm : O, A, B, M cùng thuộc 1 đường tròn.
b) Tính tỉ số OHOM .
c) Gọi E là giao điểm của CM và đường tròn (O). Chứng minh HE vuông góc với BE.
Cho điểm M nằm ngoài đường tròn ( O; R ) sao cho OM = 2R. Từ M kẻ các tiếp tuyến MA, MB với đường tròn O (A, B là các tiếp điểm ). Kẻ đường kính AC của đường tròn (O). Gọi H là giao điểm của AB và OM.
a) Chứng minh 4 điểm : O, A, B, M cùng thuộc 1 đường tròn.
b) Tính tỉ số OHOM .
c) Gọi E là giao điểm của CM và đường tròn (O). Chứng minh HE vuông góc với BE.
Câu hỏi trong đề:
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa... kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 70k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
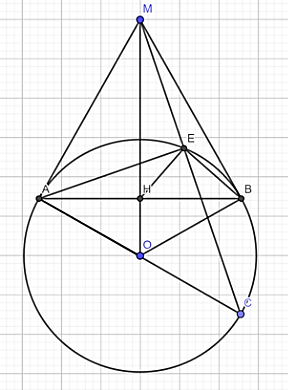
a) Vì MA, MB là tiếp tuyến của (O)
⇒ MA ⊥ OA ⇒ ^MAO = 90°
⇒ MB ⊥ OB ⇒ ^MBO = 90°
^MAO+^MBO= 90° + 90° = 180°
⇒ OAMB là tứ giác nội tiếp
⇒ O, A, B, M cùng thuộc 1 đường tròn (đpcm)
b) Vì MA, MB là tiếp tuyến của (O) kẻ từ M
⇒ M cách đều A, B mà O cách đều A, B
⇒ MO là trung trực của AB
⇒ MO ⊥ AB tại H , H là trung điểm AB
Tam giác OAM vuông tại A có đường cao AH
Suy ra: OA2 = OH.OM
⇒ OH = R22R=R2
⇒ OHOM=R22R=14
c) Áp dụng hệ thức lượng trong tam giác MAO vuông có: MA2 = MH.MO (1)
MA là tiếp tuyến nên: ^MAE=^MCA (cùng chắn cung AE)
Xét ∆MAE và ∆MCA có: ^MAE=^MCA
^AMC chung
Suy ra: ∆MAE ~ ∆MCA (g.g)
⇒ MAME=MCMA hay MA2 = MC.ME (2)
Từ (1) và (2): MC.ME = MH.MO
⇒ MHME=MCMO
Xét ∆MHE và ∆MCO có:
^OMC chung
MHME=MCMO
⇒ ∆MHE ~ ∆MCO (c.g.c)
⇒ ^MHE=^MOC
⇒ 180° – ^MHE = 180° – ^MOC hay ^HEC=^AOM
Lại có: BEAC là tứ giác nội tiếp (O) do 4 điểm đều nằm trên đường tròn nên ^BEC=^BAC (cùng nhìn cạnh BC)
Lại có theo phần a: OBMA là tứ giác nội tiếp nên ^OMB=^BAO ; ^ABO=^OMA
Suy ra: ^BEC=^OMB
Lại có: ^ABO=^OMB (Cùng phụ với ^MBA )
Mà ^ABO=^OMA
Suy ra: ^BEC=^OMA
^HEB=^HEC+^BEC=^AOM+^OMA
= 90°
Vậy HE vuông góc với BE.
Nhà sách VIETJACK:
Sách - 250+ Công thức giải nhanh môn Toán 12 Vietjack theo chương trình mới cho 2k7
Đã bán 1,3k
₫ 36.000
₫ 18.000
Combo - Sách 20 Bộ đề, Tổng ôn, sổ tay ôn thi 2025 môn Toán (3 quyển) - Mới nhất cho 2k7
Đã bán 386
₫ 110.000
₫ 55.000
Combo - Sổ tay Lý thuyết trọng tâm lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL
Đã bán 1,5k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Để hoàn thành một công việc hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc?
Để hoàn thành một công việc hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc?
Xem đáp án »
12/07/2024
47,694
Câu 4:
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg chất B. Từ mỗi tấn nguyên liệu loại II giá triệu đồng có thể chiết xuất được 10kg chất A và 1,5kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại
Xem đáp án »
12/07/2024
39,018
Câu 5:
cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.
cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.
Xem đáp án »
13/07/2024
31,869
Câu 6:
Chứng minh điểm G là trọng tâm của tam giác ABC khi và chỉ khi →GA+→GB+→GC=→0 .
Chứng minh điểm G là trọng tâm của tam giác ABC khi và chỉ khi →GA+→GB+→GC=→0 .
Xem đáp án »
13/07/2024
30,192
Câu 7:
Một công ty cần thuê xe để chở 120 người và 6,5 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 9 chiếc và loại xe B có 8 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi chiếc xe loại A có thể chở tối đa 20 người và 0,5 tấn hàng; mỗi chiếc xe loại B có thể chở tối đa 10 người và 2 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là thấp nhất?
Một công ty cần thuê xe để chở 120 người và 6,5 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 9 chiếc và loại xe B có 8 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi chiếc xe loại A có thể chở tối đa 20 người và 0,5 tấn hàng; mỗi chiếc xe loại B có thể chở tối đa 10 người và 2 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là thấp nhất?
Xem đáp án »
12/07/2024
27,654
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
-
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận