Câu hỏi:
21/06/2024 455Trong không gian Oxyz,Oxyz, cho mặt phẳng (P)(P) cắt các tia Ox,Oy,OzOx,Oy,Oz lần lượt tại ba điểm A(1;0;0),A(1;0;0),B(0;b;0),B(0;b;0),C(0;0;c).C(0;0;c). Biết mặt phẳng (P)(P) vuông góc với mặt phẳng (Q):y−z+1=0(Q):y−z+1=0 và khoảng cách từ OO đến (P)(P) bằng 13.13. Khi đó tích 4bc4bc bằng
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có (P):x1+yb+zc=1⇔x+yb+zc−1=0(P):x1+yb+zc=1⇔x+yb+zc−1=0.
Vì (P)(P) vuông góc với mặt phẳng (Q)(Q) nên 1⋅0+1y⋅1+1c⋅(−1)=0⇔b=c1⋅0+1y⋅1+1c⋅(−1)=0⇔b=c.
Lại có d(O;(P))=1√1+1b2+1c2=13⇔1+2b2=9⇔[b=12=cb=−12=c.
Suy ra 4bc=4⋅12⋅12=4⋅(−12)⋅(−12)=1. Chọn A.
Sách thầy cô Vietjack biên soạn
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
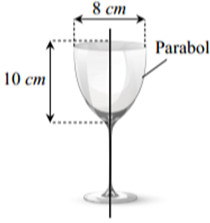
Một cốc rượu có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc (bố dọc cốc thành 2 phần bằng nhau) là một đường parabol. Tính thể tích cm3 tối đa mà cốc có thể chứa được (làm tròn đến hàng đơn vị).
Xem đáp án »
13/07/2024
37,110
Câu 2:
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−25;25] sao cho đồ thị hàm số y=x−1x2−2mx+3m+10 có đúng 2 đường tiệm cận đứng?
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−25;25] sao cho đồ thị hàm số y=x−1x2−2mx+3m+10 có đúng 2 đường tiệm cận đứng?
Xem đáp án »
21/06/2024
12,017
Câu 3:
Lĩnh vực nào sau đây không đặt ra làm mục tiêu hợp tác chính trong Liên minh châu Âu (EU)?
Xem đáp án »
08/08/2024
8,908
Câu 4:
Có bao nhiêu số nguyên m để phương trình 3cos(x+π6)−m+5=0 có nghiệm?
Xem đáp án »
21/06/2024
5,442
Câu 6:
Cho hàm số f(x)=2|x−1|. Gọi F(x) là một nguyên hàm của hàm số f(x) thỏa mãn F(2)+F(0)=5. Giá trị của biểu thức P=F(3)+F(−2) bằng
Cho hàm số f(x)=2|x−1|. Gọi F(x) là một nguyên hàm của hàm số f(x) thỏa mãn F(2)+F(0)=5. Giá trị của biểu thức P=F(3)+F(−2) bằng
Xem đáp án »
21/06/2024
3,654
Câu 7:
Khó khăn lớn nhất của Đông Nam Bộ trong phát triển nông nghiệp là
Xem đáp án »
08/08/2024
3,003
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 8)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận