Câu hỏi:
12/11/2024 671Cho nửa đường tròn (O;R), đường kính AB. Vẽ nửa đường tròn tâm O′, đường kính AO (cùng phía với nửa đường tròn (O)). Một đường thẳng bất kì qua A cắt (O),(O′) lần lượt tại C,D. Nếu BC là tiếp tuyến của nửa đường tròn (O′) thì
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
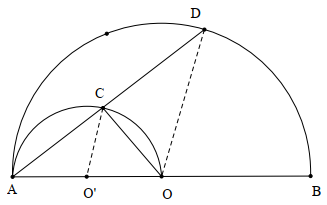
Vì đường tròn tâm O′ có AO là đường kính nên O′C=O′O=AO2=R2.
Ta có OB=R và O′B=OO′+OB=R2+R=3R2.
Vì BC là tiếp tuyến của nửa đường tròn (O′) nên O′C⊥BC tại C.
Áp dụng định lí Pythagore cho tam giác O′BC vuông tại C, ta được O′B2=O′C2+BC2.
Suy ra BC2=O′B2−O′C2=(3R2)2−(R2)2=2R2.
Do đó BC=R√2.
Vậy ta chọn phương án B.
Nhà sách vietjack
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho đường tròn (O1) và (O2) tiếp xúc ngoài tại A và một đường thẳng (d) tiếp xúc với (O1),(O2) lần lượt tại B,C. Tam giác ABC là
Xem đáp án »
12/11/2024
1,022
Câu 2:
III. Vận dụng
Cho hai đường tròn (O;5cm) và (I;R) với R<5cm. Biết OI=3cm, giá trị của R để hai đường tròn tiếp xúc trong là
Xem đáp án »
12/11/2024
913
Câu 3:
Cho đường tròn (O) và (O′) tiếp xúc ngoài tại A. Kẻ đường kính AB của đường tròn (O) và đường kính AC của đường tròn (O′). Gọi DE là tiếp tuyến của cả hai đường tròn (O) và (O′) với hai tiếp điểm D∈(O) và E∈(O′) (DE không cắt đoạn O′O). Gọi M là giao điểm của BD và CE. Biết rằng ^DOA=60∘ và OA=6cm. Diện tích tứ giác ADME bằng
Xem đáp án »
12/11/2024
369
Câu 4:
Cho tam giác ABC vuông tại A, vẽ đường tròn (B;BA) và đường tròn (C;CA) chúng cắt nhau tại D (D khác A). Kết luận nào sau đây đúng nhất?
Xem đáp án »
12/11/2024
339
Câu 5:
Cho hai đường tròn (O;5cm) và (I;R). Biết OI=7cm, giá trị của R để hai đường tròn ở ngoài nhau là
Xem đáp án »
12/11/2024
330
Câu 6:
Cho hai đường tròn (O;R) và (O′;r) với R>r. Ta nói hai đường tròn (O;R) và (O′;r) ở ngoài nhau khi
Xem đáp án »
12/11/2024
247
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 03
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận