Câu hỏi:
19/01/2025 1,359
Trong không gian Oxyz, cho ba điểm A(−1;1;2),B(3;2;2),C(−1;6;0). Xét M(a;b;0) trên mặt phẳng (Oxy) sao cho biểu thức S=2MA+|→MB+→MC| đạt giá trị nhỏ nhất. Khi đó a+b bằng bao nhiêu (làm tròn kết quả đến hàng phần mười)?
Trong không gian Oxyz, cho ba điểm A(−1;1;2),B(3;2;2),C(−1;6;0). Xét M(a;b;0) trên mặt phẳng (Oxy) sao cho biểu thức S=2MA+|→MB+→MC| đạt giá trị nhỏ nhất. Khi đó a+b bằng bao nhiêu (làm tròn kết quả đến hàng phần mười)?
Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trung điểm của BC là I(1;4;1). Ta có S=2MA+|2→MI|=2(MA+MI).
Do điểm A và điểm I nằm cùng phía so với mặt phẳng (Oxy) nên MA+MI=MA′+MI với A′(−1;1;−2) là điểm đối xứng của A qua mặt phẳng (Oxy).
Ta lại có S=2(MA′+MI)≥2A′I. Suy ra M∈(Oxy) và M,A′,I thẳng hàng.
Khi đó, hai vectơ →A′M=(a+1;b−1;2), →A′I=(2;3;3) cùng phương.
Suy ra a+12=b−13=23⇒{a=13b=3. Vậy a+b=103≈3,3.
Đáp án: 3,3.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Khi đặt hệ tọa độ Oxyzvào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu (S) (tập hợp những điểm nằm trong và nằm trên mặt cầu tương ứng). Biết mặt cầu (S) có phương trình: x2+y2+z2−2x−4y−6z+5=0. Khoảng cách xa nhất giữa hai vùng phủ sóng là bao nhiêu kilômét?
![Khi đặt hệ tọa độ \[Oxyz\]vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid44-1737301480.png)
Khi đặt hệ tọa độ Oxyzvào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu (S) (tập hợp những điểm nằm trong và nằm trên mặt cầu tương ứng). Biết mặt cầu (S) có phương trình: x2+y2+z2−2x−4y−6z+5=0. Khoảng cách xa nhất giữa hai vùng phủ sóng là bao nhiêu kilômét?
Xem đáp án »
19/01/2025
42,386
Câu 2:
Một chiếc bát thủy tinh có bề dày của phần xung quanh là một khối tròn xoay, khi xoay hình phẳng D quanh một đường thẳng a bất kì nào đó mà khi gắn hệ trục tọa độ Oxy (đơn vị trên trục là decimét) vào hình phẳng D tại một vị trí thích hợp, thì đường thẳng a sẽ trùng với trục Ox. Khi đó hình phẳng D được giới hạn bởi các đồ thị hàm số y=x+1x, y=x và hai đường thẳng x=1, x=4. Thể tích của bề dày chiếc bát thủy tinh đó bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng phần mười)?
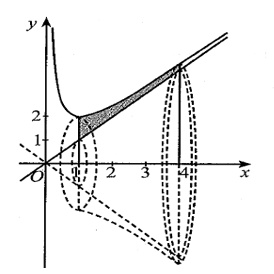
Một chiếc bát thủy tinh có bề dày của phần xung quanh là một khối tròn xoay, khi xoay hình phẳng D quanh một đường thẳng a bất kì nào đó mà khi gắn hệ trục tọa độ Oxy (đơn vị trên trục là decimét) vào hình phẳng D tại một vị trí thích hợp, thì đường thẳng a sẽ trùng với trục Ox. Khi đó hình phẳng D được giới hạn bởi các đồ thị hàm số y=x+1x, y=x và hai đường thẳng x=1, x=4. Thể tích của bề dày chiếc bát thủy tinh đó bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng phần mười)?
Xem đáp án »
19/01/2025
16,030
Câu 3:
Xác suất bắn trúng đích của xạ thủ hạng I là 0,8 và của xạ thủ hạng II là 0,7. Chọn ngẫu nhiên 1 xạ thủ từ một nhóm gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xạ thủ này bắn một viên đạn và viên đạn đó trúng mục tiêu, tính xác suất để đó là xạ thủ hạng I (làm tròn kết quả đến hàng phần trăm).
Xác suất bắn trúng đích của xạ thủ hạng I là 0,8 và của xạ thủ hạng II là 0,7. Chọn ngẫu nhiên 1 xạ thủ từ một nhóm gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xạ thủ này bắn một viên đạn và viên đạn đó trúng mục tiêu, tính xác suất để đó là xạ thủ hạng I (làm tròn kết quả đến hàng phần trăm).
Xem đáp án »
19/01/2025
8,895
Câu 4:
Diện tích hình phẳng giới hạn bởi parabol (P):y=f(x)=x2−1, trục tung và tiếp tuyến của (P) tại điểm M(−1;0) bằng
Xem đáp án »
19/01/2025
4,576
Câu 5:
Bất phương trình log3(x2−x+7)<2 có tập nghiệm là khoảng (a;b). Tính b−a.
Xem đáp án »
19/01/2025
3,155
Câu 6:
Trong không gian Oxyz, cho hai điểm A(1;2;3), B(0;1;−6) và mặt phẳng (P):4x−y+2z+13=0.
a) Mặt phẳng (P) đi qua điểm A.
b) Đường thẳng Δ đi qua điểm A và vuông góc với mặt phẳng (P) có phương trình tham số là {x=1+4ty=2+tz=3+2t.
c) Điểm C(−3;3;1) là giao điểm của đường thẳng Δ và mặt phẳng (P).
d) Gọi d là một đường thẳng nằm trong (P) và d đi qua B sao cho khoảng cách từ A đến d đạt giá trị nhỏ nhất. Một vectơ chỉ phương của d có tọa độ là (a;b;c) với a là số nguyên tố. Giá trị của a+b+c=6.
Trong không gian Oxyz, cho hai điểm A(1;2;3), B(0;1;−6) và mặt phẳng (P):4x−y+2z+13=0.
a) Mặt phẳng (P) đi qua điểm A.
b) Đường thẳng Δ đi qua điểm A và vuông góc với mặt phẳng (P) có phương trình tham số là {x=1+4ty=2+tz=3+2t.
c) Điểm C(−3;3;1) là giao điểm của đường thẳng Δ và mặt phẳng (P).
d) Gọi d là một đường thẳng nằm trong (P) và d đi qua B sao cho khoảng cách từ A đến d đạt giá trị nhỏ nhất. Một vectơ chỉ phương của d có tọa độ là (a;b;c) với a là số nguyên tố. Giá trị của a+b+c=6.
Xem đáp án »
19/01/2025
2,620
Câu 7:
Trong không gian tọa độ Oxyz, mặt cầu (S) có tâm I(2;1;−1) và đường kính 6 có phương trình là
Xem đáp án »
19/01/2025
2,088
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
45 bài tập Xác suất có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận