Câu hỏi:
11/03/2025 219
(4,0 điểm)
2) Cho đường tròn (O) đường kính AB=2R. Lấy điểm C trên đường tròn (O) và lấy điểm M bất kì trên cung nhỏ BC (M không trùng với B,C). Gọi H là giao điểm của AM và BC. Đường thẳng AC cắt đường thẳng BM tại D. DH cắt AB tại K.
a) Chứng minh rằng bốn điểm C, D, M, H cùng thuộc một đường tròn.
(4,0 điểm)
2) Cho đường tròn (O) đường kính AB=2R. Lấy điểm C trên đường tròn (O) và lấy điểm M bất kì trên cung nhỏ BC (M không trùng với B,C). Gọi H là giao điểm của AM và BC. Đường thẳng AC cắt đường thẳng BM tại D. DH cắt AB tại K.
a) Chứng minh rằng bốn điểm C, D, M, H cùng thuộc một đường tròn.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k).
Quảng cáo
Trả lời:
a) Xét đường tròn (O;R) có ^ACB là góc nội tiếp chắn nửa đường tròn nên ^ACB=90°, hay AC⊥CB suy ra ^DCH=90° hay tam giác DCH vuông tại C suy ra ba điểm D,C,H cùng thuộc đường tròn ngoại tiếp tam giác DCH có tâm là trung điểm của DH và bán kính bằng 12DH (đường tròn đường kính DH)
Chứng minh tương tự ta có ba điểm D,M,H cùng thuộc đường tròn đường kính DH.Vậy bốn điểm C,D,M,H cùng thuộc đường tròn đường kính DH

Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh rằng ΔDCM đồng dạng với ΔDBA.
b) Chứng minh rằng ΔDCM đồng dạng với ΔDBA.
Lời giải của GV VietJack
b) Ta có bốn điểm A,B,M,C cùng nằm trên đường tròn (O;R) nên tứ giác ABMC nội tiếp đường tròn, suy ra ^ACM+^ABM=180° (tổng hai góc đối của tứ giác nội tiếp).
Mà ^ACM+^MCD=180° (kề bù) nên ^ABM=^MCD hay ^DBA=^DCM.
^CAM,^CBM là các góc nội tiếp chắn cung CM suy ra ^CAM=^CBM hay ^DAM=^DBC
Xét ΔDCM và ΔDBA có: ^ADB là góc chung và ^DCM=^DBA (chứng minh trên)
Do đó ΔDCM∽ΔDBA (g.g).
Câu 3:
c) Chứng minh rằng ^CKM=^COM.
c) Chứng minh rằng ^CKM=^COM.
Lời giải của GV VietJack
c) Xét đường tròn (O;R) có ^CAM, ^COM lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung CM nên ^COM=2^CAM. (1)
Chứng minh tương tự câu a ta có bốn điểm A , C , H , K cùng thuộc một đường tròn hay tứ giác ACHK nội tiếp đường tròn, nên ^CAH=^CKH (hai góc nội tiếp cùng chắn cung CH) hay ^CAM=^CKH
Chứng minh tương tự, ta có ^CBM=^MKH.
Lại có ^CAM=^CBM (hai góc nội tiếp cùng chắn cung CM của đường tròn (O)) nên ^CKH=^MKH hay KH là tia phân giác của ^CKM, suy ra ^CKM=2^CKH=2^CAM (2)
Từ (1) và (2) suy ra ^CKM=^COM.
Câu 4:
d) Kẻ phân giác góc AMB cắt AB tại P. Tìm vị trí của M thỏa mãn đề bài để MPMA+MB đạt giá trị lớn nhất.
Lời giải của GV VietJack
d) Ta có MP là tia phân giác của ^AMB nên ^AMP=^BMP=12^AMB=12⋅90°=45°.
Gọi Q là giao điểm của MP với đường tròn (O;R) Khi đó ^AQB=90° (góc nội tiếp chắn nửa đường tròn) và ^ABQ=^AMQ=45° (hai góc nội tiếp cùng chắn cung AQ của đường tròn (O))
Suy ra ΔQAB vuông cân tại Q
Do đó sin^ABQ=AQAB hay AQAB=√22 nên ABAQ=√2.Xét ΔMPA và ΔBPQ có: ^AMP=^QBP (chứng minh trên) và ^MPA=^BPQ (đối đỉnh)
Do đó ΔMPA∽ΔBPQ (g.g). Suy ra MPBP=MABQ hay MPMA=BPBQ.
Tương tự ΔMPB∽ΔAPQ (g.g), suy ra MPMB=APAQ.
Do đó MPMA+MPMB=BPBQ+APAQ=ABAQ=√2 (do BQ=AQ vì vuông cân tại Q.)
¬ Chứng minh bất đẳng thức bổ đề: Với x>0,y>0 ta luôn có 1x+1y≥4x+y.
Thật vậy, với x>0,y>0 ta có: (x−y)2≥0
x2−2xy+y2≥0
x2+2xy+y2≥4xy
(x+y)2xy(x+y)≥4xyxy(x+y)
x+yxy≥4x+y
1x+1y≥4x+y.
Dấu “=” xảy ra khi và chỉ khi (x−y)2=0 hay x=y. Bất đẳng thức trên đã được chứng minh.
Áp dụng bất đẳng thức trên, ta có: 1MA+1MB≥4MA+MB
Hay MPMA+MB≤MP⋅14(1MA+1MB)=14⋅(MPMA+MPMB)=√24.
Dấu “=” xảy ra khi và chỉ khi MA=MB.
Vậy giá trị lớn nhất của MPMA+MB là √24 khi MA=MB hay M là điểm chính giữa cung AB.
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
(2,5 điểm)
3) Cho đường thẳng (d):y=(m−2)x+3 (m≠2). Tìm m để (d) cắt Ox tại A, cắt Oy tại B mà ^BAO=60°.
Câu 3:
(2,5 điểm)
1) Trong kỳ thi môn toán lớp 9, một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát cho. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 42 tờ giấy thi. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 1 tờ giấy thi, bao nhiêu thí sinh làm bài 2 tờ giấy thi? Biết rằng có 3 thí sinh làm 3 tờ giấy thi.
(2,5 điểm)
1) Trong kỳ thi môn toán lớp 9, một phòng thi của trường có 24 thí sinh dự thi. Các thí sinh đều phải làm bài trên giấy thi của trường phát cho. Cuối buổi thi, sau khi thu bài, giám thị coi thi đếm được tổng số tờ là 42 tờ giấy thi. Hỏi trong phòng thi đó có bao nhiêu thí sinh làm bài 1 tờ giấy thi, bao nhiêu thí sinh làm bài 2 tờ giấy thi? Biết rằng có 3 thí sinh làm 3 tờ giấy thi.
Câu 4:
(0,5 điểm) Trong một xưởng cơ khí đang có sẵn những thanh thép dài 7,4m. Một công trình xây dựng đang cần có 1000 đoạn thép dài 0,7m và 2000 đoạn thép dài 0,5m (cùng kích cỡ với thép 7,4m). Em hãy tìm xem cần dùng bao nhiêu thanh thép 7,4m để thoả mãn yêu cần trên với chi phí tiết kiệm nhất.
(0,5 điểm) Trong một xưởng cơ khí đang có sẵn những thanh thép dài 7,4m. Một công trình xây dựng đang cần có 1000 đoạn thép dài 0,7m và 2000 đoạn thép dài 0,5m (cùng kích cỡ với thép 7,4m). Em hãy tìm xem cần dùng bao nhiêu thanh thép 7,4m để thoả mãn yêu cần trên với chi phí tiết kiệm nhất.
Câu 5:
(4,0 điểm)
1) Cho tam giác ABC đều có cạnh AB = 3cm nội tiếp đường tròn tâm O bán kính R. Hạ AH vuông góc với BC. Tính diện tích phần nằm trong hình tròn (O;R) và nằm ngoài tam giác ABC (phần tô đậm trong hình bên).
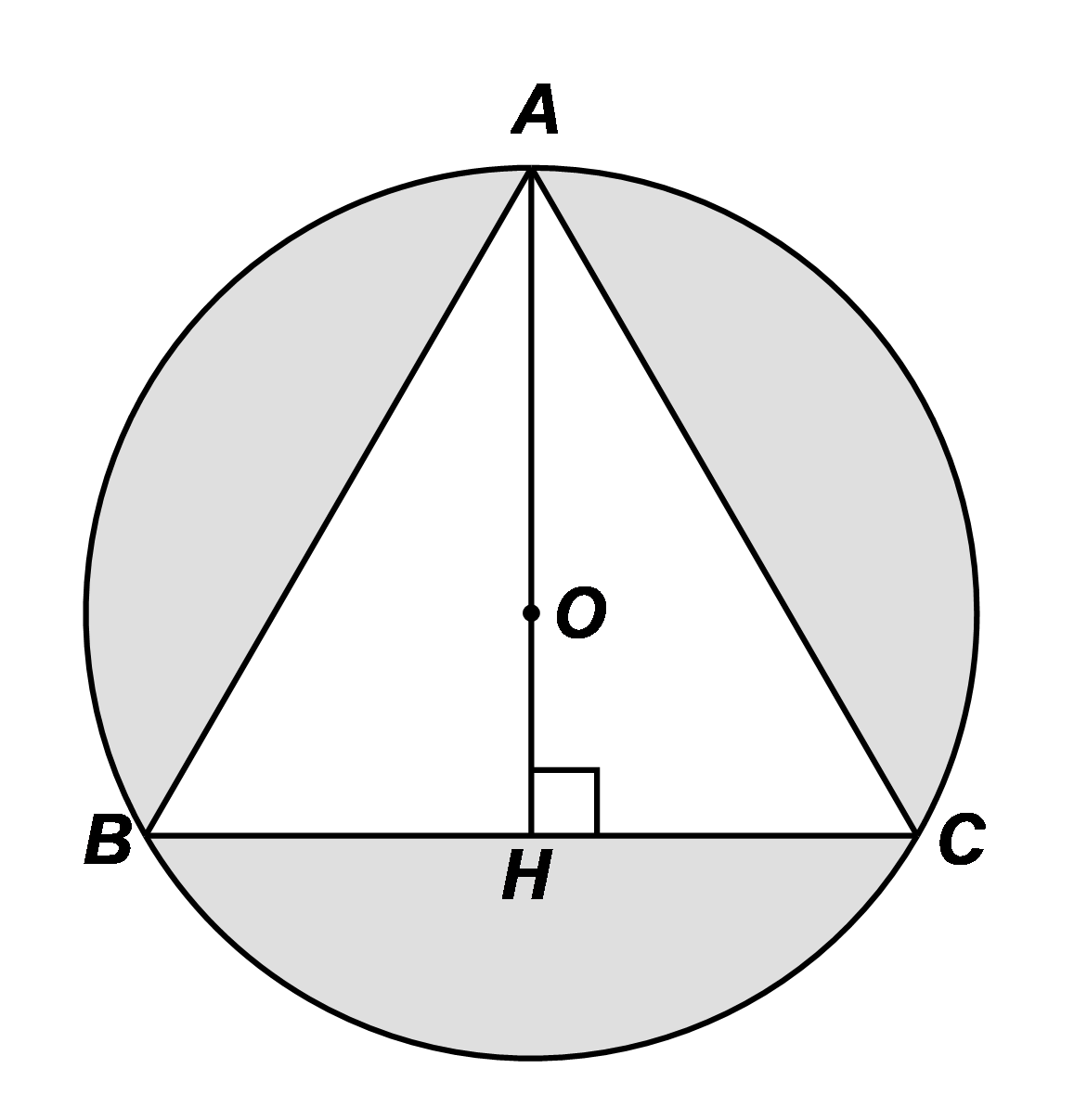
(4,0 điểm)
1) Cho tam giác ABC đều có cạnh AB = 3cm nội tiếp đường tròn tâm O bán kính R. Hạ AH vuông góc với BC. Tính diện tích phần nằm trong hình tròn (O;R) và nằm ngoài tam giác ABC (phần tô đậm trong hình bên).
Câu 6:
(1,5 điểm)
1) Biểu đồ sau cho biết số lượng các loại ô tô một cửa hàng bán được trong năm 2023:
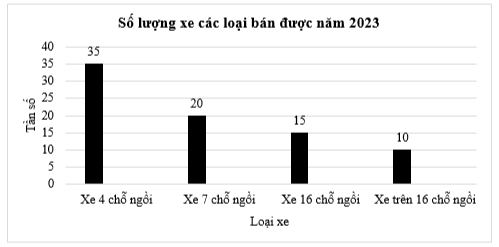
a) Lập bảng tần số cho dữ liệu được biểu diễn trên biểu đồ.
b) Giả sử tỉ lệ các loại xe bán được không đổi và cửa hàng bán được tổng số 240 ô tô các loại trong năm 2023. Hãy ước lượng số ô tô 4 chỗ cửa hàng bán được.
2) Gieo một con xúc xắc đồng chất 100 lần và ghi lại kết quả trong bảng sau:

Xét biến cố A “Số chấm xuất hiện trên mặt xúc xắc là số lẻ chia hết cho A”. Tính xác suất của biến cố A

🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 03
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 02
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án




Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận