Câu hỏi:
12/03/2025 181
Câu 12-14: (1,5 điểm) Cho tam giác nhọn ABC hai đường cao BE,CF cắt nhau tại H. Gọi M là trung điểm của BC,I là trung điểm của AH.
1) Chứng minh tứ giác AEHF nội tiếp đường tròn tâm I.
Câu 12-14: (1,5 điểm) Cho tam giác nhọn ABC hai đường cao BE,CF cắt nhau tại H. Gọi M là trung điểm của BC,I là trung điểm của AH.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét ΔAEH vuông tại E có I là trung điểm của cạnh huyền AH nên đường tròn ngoại tiếp ΔAEH là đường tròn tâm I đường kính AH.
Tương tự, đường tròn ngoại tiếp ΔAFH vuông tại F là đường tròn tâm I đường kính AH.
Như vậy, đường tròn tâm I đường kính AH đi qua các điểm A,E,H,F.
Vậy tứ giác AEHF nội tiếp đường tròn tâm I.
Câu hỏi cùng đoạn
Câu 2:
2) Chứng minh FM vuông góc với FI.
Lời giải của GV VietJack
Ta có IA=IF nên ΔIAF cân tại I. Suy ra ^IAF=^IFA. (1)
Vì tứ giác AEHF là tứ giác nội tiếp nên ^HAF=^HEF (hai góc nội tiếp cùng chắn cung HF). (2)
Chứng minh tương tự câu 1, ta cũng có tứ giác BFEC nội tiếp đường tròn tâm M đường kính FC.
Do đó ^BEF=^BCF (hai góc nội tiếp cùng chắn cung BF). (3)
Ta có MF=MC nên ΔMFC cân tại M. Suy ra ^MCF=^MFC. (4)
Từ (1), (2), (3) và (4) suy ra ^IFA=^MFC.
Lại có ^IFA+^IFC=90∘ suy ra ^MFC+^IFC=90∘ hay ^IFM=90∘ nên FM⊥FI.
Câu 3:
3) Tiếp tuyến tại các điểm B và C của đường tròn ngoại tiếp tam giác ABC cắt nhau tại điểm N. Chứng minh rằng AN đi qua trung điểm của đoạn thẳng EF.
Lời giải của GV VietJack
⦁ Do tứ giác BFEC nội tiếp đường tròn nên ^BFE+^BCE=180∘ (tổng hai góc đối nhau của tứ giác nội tiếp).
Mà ^BFE+^AFE=180∘ (hai góc kề bù) nên ^AFE=^BCE.
Xét ΔAEF và ΔABC có: ^BAC là góc chung và ^AFE=^ACB.
Do đó (g.g). Suy ra AFAC=EFBC.
Gọi P là trung điểm của EF. Khi đó, EF=2FP.
Do M là trung điểm của BC nên BC=2CM.
Do đó AFAC=EFBC=2FP2CM=FPCM.
Xét ΔAFP và ΔACM có: ^AFP=^ACM và AFAC=FPCM.
Do đó (c.g.c). Suy ra ^FAP=^CAM (hai góc tương ứng). (9)
⦁ Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Vì NB,NC là hai tiếp tuyến của đường tròn (O) nên NB=NC (tính chất hai tiếp tuyến cắt nhau), suy ra N nằm trên đường trung trực của BC.
Lại có OB=OC nên O nằm trên đường trung trực của BC.
Do đó ON là đường trung trực của BC.
Mà M là trung điểm của BC nên đường trung trực ON của BC đi qua M hay ON⊥BC tại M.
Xét ΔABC có hai đường cao BE,CF cắt nhau tại H nên H là trực tâm của tam giác, suy ra AH⊥BC.
Ta có ON⊥BC và AH⊥BC nên ON//AH. Suy ra ^HAN=^ONA (hai góc so le trong). (5)
Xét ΔOBM và ΔONB có: ^OMB=^OBN=90∘ và ^BON là góc chung
Do đó (g.g). Suy ra OBON=OMOB hay OB2=OM⋅ON.
Mà OB=OA nên OA2=OM⋅ON, suy ra OAOM=ONOA.
Xét ΔONA và ΔOAM có: ^AON là góc chung và OAOM=ONOA.
Do đó (g.g). Suy ra ^ONA=^OAM (hai góc tương ứng). (6)
Từ (5) và (6) suy ra ^HAN=^OAM. (7)
Xét ΔOAC cân tại O (do OA=OC) nên ^OAC=^OCA=180∘−^AOC2.
Lại có ^ABC,^AOC lần lượt là góc nội tiếp, góc ở tâm cùng chắn cung AC của đường tròn (O) nên ^ABC=12^AOC hay ^AOC=2^ABC.
Do đó ^OAC=180∘−2^ABC2=90∘−^ABC=90∘−^FBC.
Mà ^FBC+^FCB=90∘ (tổng hai góc nhọn của ΔFBC vuông tại F) nên ^FCB=90∘−^FBC.
Suy ra ^OAC=^FCB.
Mặt khác, ^HAF=^HEF và ^BEF=^BCF (chứng minh câu 2) nên ^HAF=^OAC. (8)
Từ (7) và (8) suy ra ^HAN+^HAF=^OAM+^OAC hay ^FAN=^CAM. (10)
⦁ Từ (9) và (10) suy ra ^FAP=^FAN hay ba điểm A,P,N thẳng hàng.
Vậy đường thẳng AN đi qua trung điểm P của EF.
Nhà sách vietjack
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
1) Hãy lập bảng tần số và bảng tần số tương đối số lỗi chính tả của học sinh.
Xem đáp án »
12/03/2025
339
Câu 3:
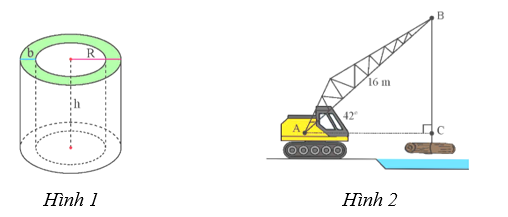
1) Một bể nước hình trụ có bán kính đáy R=1,2m (tính từ tâm bể đến mép ngoài), bề dày của thành bể là b=0,05m, chiều cao lòng bể là h=1,6m (Hình 1). Tính dung tích của bể nước (kết quả làm tròn đến hàng phần trăm).
Xem đáp án »
12/03/2025
193
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 9 Kết nối tri thức có đáp án - Đề 03
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 9 Chân trời sáng tạo có đáp án (Đề số 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận