Câu hỏi:
18/03/2025 188
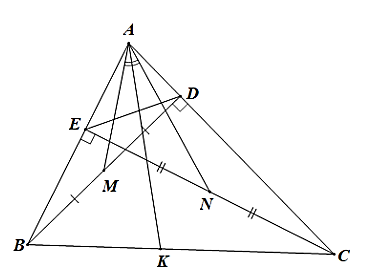
(1,5 điểm) Cho tam giác ABC có ba góc nhọn (AB<AC), vẽ các đường cao BD và CE.
a) Chứng minh rằng ΔABD∽.
(1,5 điểm) Cho tam giác ABC có ba góc nhọn (AB<AC), vẽ các đường cao BD và CE.
a) Chứng minh rằng ΔABD∽.
Câu hỏi trong đề: Bộ 5 đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Xét \Delta ABD và \Delta ACE có:
\widehat {BAC} chung (gt)
\widehat {ADB} = \widehat {AEC} = 90^\circ (gt)
Suy ra (g.g).
Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh rằng \widehat {ABC} + \widehat {EDC} = 180^\circ .
b) Chứng minh rằng \widehat {ABC} + \widehat {EDC} = 180^\circ .
Lời giải của GV VietJack
Vì (cmt) nên \frac{{AD}}{{AE}} = \frac{{AB}}{{AC}} (các cặp tương ứng tỉ lệ)
Xét \Delta AED và \Delta ACB có:
\frac{{AD}}{{AE}} = \frac{{AB}}{{AC}} (cmt)
\widehat {BAC} chung
Do đó, (c.g.c)
Suy ra \widehat {ADE} = \widehat {ABC} (hai góc tương ứng)
Mặt khác \widehat {ADE} + \widehat {EDC} = 180^\circ (hai góc kề bù)
Do đó, \widehat {ADE} + \widehat {EDC} = \widehat {ABC} + \widehat {EDC} = 180^\circ .
Câu 3:
c) Gọi M,N lần lượt là trung điểm của đoạn thẳng BD và CE. Vẽ AK là phân giác ngoài của \widehat {MAN} \left( {K \in BC} \right). Chứng minh rằng KB.AC = KC.AB.
c) Gọi M,N lần lượt là trung điểm của đoạn thẳng BD và CE. Vẽ AK là phân giác ngoài của \widehat {MAN} \left( {K \in BC} \right). Chứng minh rằng KB.AC = KC.AB.
Lời giải của GV VietJack
Vì nên \frac{{AD}}{{AE}} = \frac{{AB}}{{AC}}.
Mà M,N lần lượt là trung điểm của đoạn thẳng BD và CE nên BD = 2BM và CE = 2CN.
Suy ra \frac{{AB}}{{AC}} = \frac{{BD}}{{CE}} = \frac{{2BM}}{{2CN}} = \frac{{BM}}{{CN}}.
Xét \Delta ABD và \Delta ACN có: \frac{{BM}}{{CN}} = \frac{{AB}}{{AC}} (cmt)
\widehat {ABM} = \widehat {ACN} (cùng phụ với \widehat {BAC})
Do đó, (c.g.c)
Suy ra \widehat {BAM} = \widehat {CAN} (hai góc tương ứng)
Lại có AK là tia phân giác của \widehat {MAN} (giả thiết)
Suy ra \widehat {KAM} = \widehat {KAN} (tính chất tia phân giác của một góc)
Do đó, \widehat {KAM} + \widehat {BAM} = \widehat {KAN} + \widehat {CAN} hay \widehat {BAK} = \widehat {KAC}.
Nên AK là tia phân giác của \widehat {BAC}.
Theo tính chất tia phân giác của tam giác, ta có: \frac{{AB}}{{AC}} = \frac{{KB}}{{KC}}.
Do đó, KB.AC = KC.AB (điều phải chứng minh).
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Gọi S là tập hợp các số tự nhiên có ba chữ số đôi một khác nhau được lập thành từ các số 1,2,3,4,6. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn chia hết cho 3.
(Kết quả ghi dưới dạng số thập phân)
Gọi S là tập hợp các số tự nhiên có ba chữ số đôi một khác nhau được lập thành từ các số 1,2,3,4,6. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn chia hết cho 3.
(Kết quả ghi dưới dạng số thập phân)
Xem đáp án »
18/03/2025
732
Câu 4:
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Thống kê số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong các năm 2015; 2018; 2019; 2020 bằng bảng dưới đây.
Năm
2015
2018
2019
2020
Số lượt hành khách
(triệu lượt người)
36,4
53,7
58,8
19,1
(Nguồn: Niên giám thống kê 2021)
Hỏi số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa năm 2020 giảm bao nhiêu phần trăm so với năm 2019? (Kết quả làm tròn đến hàng phần mười)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Thống kê số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong các năm 2015; 2018; 2019; 2020 bằng bảng dưới đây.
|
Năm |
2015 |
2018 |
2019 |
2020 |
|
Số lượt hành khách (triệu lượt người) |
36,4 |
53,7 |
58,8 |
19,1 |
(Nguồn: Niên giám thống kê 2021)
Hỏi số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa năm 2020 giảm bao nhiêu phần trăm so với năm 2019? (Kết quả làm tròn đến hàng phần mười)
Xem đáp án »
18/03/2025
325
Câu 5:
Giữa hai điểm B và C bị ngăn cách bởi hồ nước (như hình vẽ).
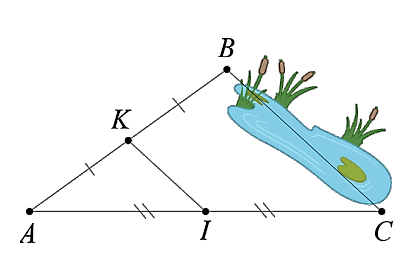
Xác định độ dài của BC mà không cần phải di chuyển qua hồ nước. Biết rằng đoạn thẳng KI dài 25{\rm{ m}} và K là trung điểm của AB, I là trung điểm của AC. (Đơn vị: m).
Giữa hai điểm B và C bị ngăn cách bởi hồ nước (như hình vẽ).
Xác định độ dài của BC mà không cần phải di chuyển qua hồ nước. Biết rằng đoạn thẳng KI dài 25{\rm{ m}} và K là trung điểm của AB, I là trung điểm của AC. (Đơn vị: m).
Xem đáp án »
18/03/2025
301
🔥 Đề thi HOT:
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
10 Bài tập Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh (có lời giải)
-
Đề kiểm tra Cuối kì 2 Toán 8 CTST có đáp án (Đề 1)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận