Câu hỏi:
16/07/2020 758Cho hàm số F(x) là một nguyên hàm của hàm số f(x)=2cosx−1sin2x trên khoảng (0;π) Biết rằng giá trị lớn nhất của F(x) trên khoảng (0;π) là √3. Chọn mệnh đề đúng trong các mệnh đề sau?
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A.
Nhà sách vietjack
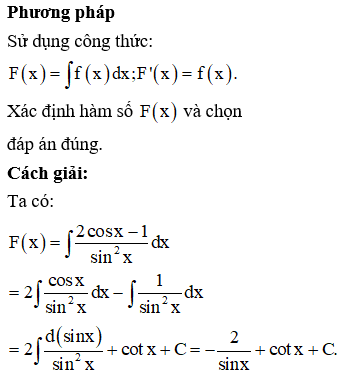
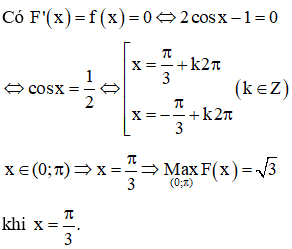
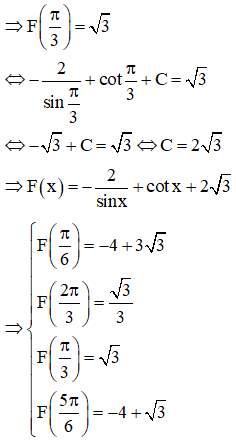
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số f(x) có đạo hàm trên R là f'(x)=(x−1)(x+3). Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;20] để hàm số y=f(x2+3x−m) đồng biến trên khoảng (0;2)?
Xem đáp án »
16/07/2020
46,844
Câu 2:
Gieo đồng thời hai con súc sắc cân đối và đồng chất. Tính xác suất P để hiệu số chấm trên các mặt xuất hiện của hai con súc sắc bằng 2.
Xem đáp án »
16/07/2020
16,133
Câu 3:
Gọi T là tổng các nghiệm của phương trình log213x−log3x+4=0. Tính T.
Xem đáp án »
16/07/2020
5,068
Câu 4:
Cho hàm số y=13x3−2mx2+(m−1)x+2m2+1 (m là tham số). Xác định khoảng cách lớn nhất từ gốc tọa độ O(0;0) đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số trên.
Xem đáp án »
16/07/2020
4,150
Câu 5:
Tìm số giá trị nguyên thuộc đoạn [-2019;2019] của tham số m để đồ thị hàm số y=√x−3x2+x−m có đúng hai đường tiệm cận.
Xem đáp án »
16/07/2020
3,830
Câu 6:
Tìm tất cả các giá trị của tham số m để phương trình 13|cos3x|−3cos2x+5|cosx|−3+2m=0
có đúng bốn nghiệm phân biệt thuộc đoạn [0;2π].
Xem đáp án »
16/07/2020
3,709
Câu 7:
Tính tổng T của các giá trị nguyên của tham số m để phương trình ex+(m2−m)e−x=2m có đúng hai nghiệm phân biệt nhỏ hơn 1loge.
Xem đáp án »
16/07/2020
3,661
🔥 Đề thi HOT:
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
45 bài tập Xác suất có lời giải
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận