Câu hỏi:
09/04/2022 273
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm H (1;-2;3) và cắt các trục tọa độ tại các điểm A, B và C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm H (1;-2;3) và cắt các trục tọa độ tại các điểm A, B và C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án A
Gọi A(a;0;0)∈Ox,B(0;b;0)∈Oy,C(0;0;c)∈Oz.
Phương trình mặt chắn của (P):xa+yb+zc=1.
Ta có: →AH=(1−a;−2;3),→BH=(1;−2−b;3),→BC=(0;−b;c),→AC=(−a;0;c).
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Mặt phẳng (α) đi qua A, B và trung điểm M của SC. Mặt phẳng (α) chia khối chóp đã cho thành hai phần có thể tích lần lượt là V1,V2 với V1<V2. Tính tỉ số V1V2.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Mặt phẳng (α) đi qua A, B và trung điểm M của SC. Mặt phẳng (α) chia khối chóp đã cho thành hai phần có thể tích lần lượt là V1,V2 với V1<V2. Tính tỉ số V1V2.
Xem đáp án »
17/05/2022
3,141
Câu 2:
Cho hàm số f(x) liên tục và nhận giá trị dương trên [0;1]. Biết f(x).f(1−x)=1 với ∀x∈[0;1]. Tính giá trị I=1∫0dx1+f(x)
Cho hàm số f(x) liên tục và nhận giá trị dương trên [0;1]. Biết f(x).f(1−x)=1 với ∀x∈[0;1]. Tính giá trị I=1∫0dx1+f(x)
Xem đáp án »
17/05/2022
2,697
Câu 3:
Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây. Có bao nhiêu giá trị nguyên của tham số m để hàm sốy=[f(x+2018)+m2] có 5 điểm cực trị?
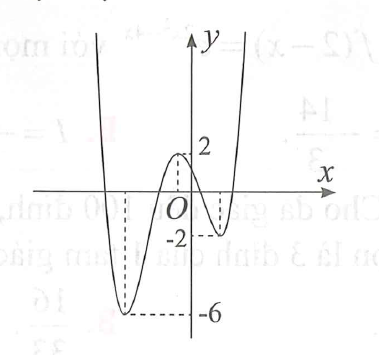
Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây. Có bao nhiêu giá trị nguyên của tham số m để hàm sốy=[f(x+2018)+m2] có 5 điểm cực trị?
Xem đáp án »
31/05/2022
2,372
Câu 4:
Tìm tất cả các giá trị của tham số m để hàm số y=2cosx+32cosx−m nghịch biến trên khoảng (0;π3).
Tìm tất cả các giá trị của tham số m để hàm số y=2cosx+32cosx−m nghịch biến trên khoảng (0;π3).
Xem đáp án »
17/05/2022
1,659
Câu 6:
Phương trình |x2−2x|(|x|−1)=m (với m là tham số thực) có tối đa bao nhiêu nghiệm thực?
Phương trình |x2−2x|(|x|−1)=m (với m là tham số thực) có tối đa bao nhiêu nghiệm thực?
Xem đáp án »
31/05/2022
1,301
Câu 7:
Cho hàm số f(x) nhận giá trị dương, có đạo hàm liên tục trên [0;2] . Biết f(0)=1 và f(x).f(2−x)=e2x2−4x với mọi x∈[0;2]. Tính tích phân I=2∫0(x3−3x2).f'
Xem đáp án »
17/05/2022
817
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
45 bài tập Xác suất có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận