Câu hỏi:
12/04/2022 992
Cho z1, z2 là nghiệm phương trình |6−3i+iz|=|2z−6−9i| và thỏa mãn |z1−z2|=85. Giá trị lớn nhất của |z1+z2| bằng
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi z1=x1+y1i, z2=x2+y2i, với x1,y1,x2,y2∈ℝ.
Do |z1−z2|=85⇒|(x1−x2)+(y1−y2)i|=85⇒√(x1−x2)2+(y1−y2)2=85
Gọi M1(x1;y1), M2(x2;y2)⇒M1M2=√(x1−x2)2+(y1−y2)2=85.
Mà z1 là nghiệm phương trình |6−3i+iz|=|2z−6−9i|
Do |z1−z2|=85⇒|(x1−x2)+(y1−y2)i|=85⇒√(x1−x2)2+(y1−y2)2=85
Gọi M1(x1;y1), M2(x2;y2)⇒M1M2=√(x1−x2)2+(y1−y2)2=85.
Mà z1 là nghiệm phương trình |6−3i+iz|=|2z−6−9i|
⇒|(6−y1)+(x1−3)i|=|(2x1−6)+(2y1−9)i|⇒√(6−y1)2+(x1−3)2=√(2x1−6)2+(2y1−9)2
⇔x12+y12−6x1−8y1+24=0⇒M1(x1;y1)∈ đường tròn (C):x2+y2−6x−8y+24=0.
Tương tự M2(x2;y2)∈(C).
Đường tròn (C) có tâm I(3;4), bán kính R=1.
Goị M là trung điểm M1M2, ⇒IM⊥M1M2, IM=√R2−M1M2=√1−(45)2=35 và |z1+z2|=2OM.
Mà OM≤OI+IM, dấu bằng xảy ra khi O, I,M thẳng hàng. Khi đó OM⊥M1M2, và OM=OI+IM=285.
⇔|z1+z2|đạt giá trị lớn nhất bằng 2(OI+IM), bằng 565.
Hoặc đánh giá chọn đáp án như sau:
Gọi N(−x2;−y2)⇒NM1=√(x1+x2)2+(y1+y2)2=|z1+z2|
Và N đối xứng với M2 qua gốc tọa độ O, N∈ đường tròn (C1):x2+y2+6x+8y+24=0.
(C1) có tâm I1(−3;−4), bán kính R1=1, (C1) đối xứng với (C) qua gốc tọa độ O.
Có I1I=10⇒I1I−R−R1=8.
Nhận xét: với mọi điểm M1∈(C), N∈(C1) thì M1N≥ I1I−R−R1. Loại các đáp án B,C,D
⇔|z1+z2|=M1Nđạt giá trị lớn nhất bằng 565.
⇔x12+y12−6x1−8y1+24=0⇒M1(x1;y1)∈ đường tròn (C):x2+y2−6x−8y+24=0.
Tương tự M2(x2;y2)∈(C).
Đường tròn (C) có tâm I(3;4), bán kính R=1.
Goị M là trung điểm M1M2, ⇒IM⊥M1M2, IM=√R2−M1M2=√1−(45)2=35 và |z1+z2|=2OM.
Mà OM≤OI+IM, dấu bằng xảy ra khi O, I,M thẳng hàng. Khi đó OM⊥M1M2, và OM=OI+IM=285.
⇔|z1+z2|đạt giá trị lớn nhất bằng 2(OI+IM), bằng 565.
Hoặc đánh giá chọn đáp án như sau:
Gọi N(−x2;−y2)⇒NM1=√(x1+x2)2+(y1+y2)2=|z1+z2|
Và N đối xứng với M2 qua gốc tọa độ O, N∈ đường tròn (C1):x2+y2+6x+8y+24=0.
(C1) có tâm I1(−3;−4), bán kính R1=1, (C1) đối xứng với (C) qua gốc tọa độ O.
Có I1I=10⇒I1I−R−R1=8.
Nhận xét: với mọi điểm M1∈(C), N∈(C1) thì M1N≥ I1I−R−R1. Loại các đáp án B,C,D
⇔|z1+z2|=M1Nđạt giá trị lớn nhất bằng 565.
Chọn đáp án B
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
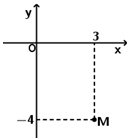
Điểm M trong hình vẽ bên là điểm biểu diễn của số phức nào dưới đây?
Xem đáp án »
12/04/2022
6,954
Câu 4:
Trong không gian với hệ tọa độ Oxyz, đường thẳng nào sau đây nhận →u=(2;1;1) là một vectơ chỉ phương?
Xem đáp án »
12/04/2022
3,462
Câu 6:
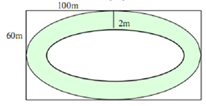
Sân chơi cho trẻ em hình chữ nhật có chiều dài 100m và chiều rộng là 60m. Người ta làm một con đường nằm trong sân . Biết viền ngoài và viền trong của con đường là hai đường elip, elip của viền ngoài có trục lớn và trục bé lần lượt song song với các cạnh của hình chữ nhật và chiều rộng của mặt đường là 2m. Kinh phí của mỗi m2 làm đường là 600.000 đồng. Tính tổng số tiền làm con đường đó
Xem đáp án »
12/04/2022
1,661
🔥 Đề thi HOT:
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
45 bài tập Xác suất có lời giải
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận