Câu hỏi:
21/05/2022 454
Cho hàm số bậc ba y =f(x) có đồ thị như hình vẽ. Gọi m là số nghiệm thực của phương trình: √f[4f(x)−7]−12f(x)+24=8−4f(x)√f[4f(x)−7]−12f(x)+24=8−4f(x) .
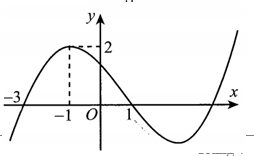
Khẳng định nào sau đây đúng?
Cho hàm số bậc ba y =f(x) có đồ thị như hình vẽ. Gọi m là số nghiệm thực của phương trình: √f[4f(x)−7]−12f(x)+24=8−4f(x)√f[4f(x)−7]−12f(x)+24=8−4f(x) .
Khẳng định nào sau đây đúng?
Đáp án chính xác
Câu hỏi trong đề: 25 đề thi thử Toán THPT Quốc gia có lời giải chi tiết !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án C
Đặt t=4f(x)−7⇒√f(t)−3t+3=1−tt=4f(x)−7⇒√f(t)−3t+3=1−t . Khi đó {t≤1f(t)=t2+t−2.
Vẽ đồ thị hàm số f(x) và y=t2+t−2 trên hệ trục tọa độ.
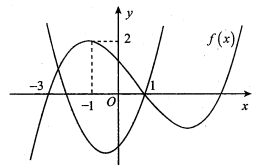
Phương trình f(t)−y=0 có nghiệm ⇔[t=1t=a (−3<a<−1)⇒[f(x)=2f(x)=a+74.
Nhìn đồ thị, ta xét phương trình f(x)=2 có 2 nghiệm.
Vì −3<a<−1⇒1<a+74<32 nên phương trình f(x)=a+74 có 3 nghiệm.
Vậy phương trình đã cho có 5 nghiệm hay m =5.
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian Oxyz, cho hai mặt phẳng(P):3x−2y+2z−5=0 và(Q):4x+5y−z+1=0 . Các điểm A, B phân biệt cùng thuộc giao tuyến của hai mặt phẳng (Q) và (P). Khi đó →AB cùng phương với vectơ nào sau đây?
Trong không gian Oxyz, cho hai mặt phẳng(P):3x−2y+2z−5=0 và(Q):4x+5y−z+1=0 . Các điểm A, B phân biệt cùng thuộc giao tuyến của hai mặt phẳng (Q) và (P). Khi đó →AB cùng phương với vectơ nào sau đây?
Xem đáp án »
21/05/2022
1,797
Câu 2:
Người ta cần làm một hộp theo dạng một khối lăng trụ đều không nắp với thể tích lớn nhất từ một miếng tôn hình vuông có cạnh là 1 mét. Thể tích của hộp cần làm là:
Người ta cần làm một hộp theo dạng một khối lăng trụ đều không nắp với thể tích lớn nhất từ một miếng tôn hình vuông có cạnh là 1 mét. Thể tích của hộp cần làm là:
Xem đáp án »
21/05/2022
1,173
Câu 4:
Cho hàm số y=f(x) có bảng biến thiên như sau:
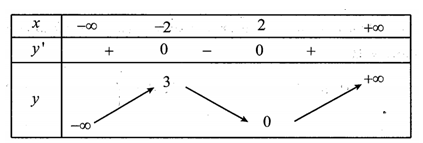
Đồ thị hàm số y=1f(2020−x)−2 có bao nhiêu tiệm cận đứng?
Cho hàm số y=f(x) có bảng biến thiên như sau:
Đồ thị hàm số y=1f(2020−x)−2 có bao nhiêu tiệm cận đứng?
Xem đáp án »
21/05/2022
575
Câu 5:
Cho F(x) là một nguyên hàm của f(x) trên [0;1], biết F(1)=2 và 1∫−1(x+1)F(x)dx=1 . Giá trị tích phân S=1∫−1(x+1)2f(x)dx là:
Cho F(x) là một nguyên hàm của f(x) trên [0;1], biết F(1)=2 và 1∫−1(x+1)F(x)dx=1 . Giá trị tích phân S=1∫−1(x+1)2f(x)dx là:
Xem đáp án »
21/05/2022
569
Câu 7:
Cho hàm số f(x) liên tục trên R và có đồ thị như hình vẽ. Biết rằng diện tích các hình phẳng (A),(B) lần lượt bằng 3 và 7. Tích phân π2∫0cosx.f(5sinx−1)dx bằng:
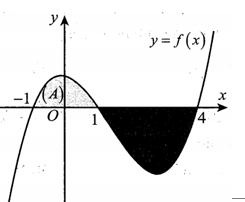
Cho hàm số f(x) liên tục trên R và có đồ thị như hình vẽ. Biết rằng diện tích các hình phẳng (A),(B) lần lượt bằng 3 và 7. Tích phân π2∫0cosx.f(5sinx−1)dx bằng:
Xem đáp án »
21/05/2022
460
🔥 Đề thi HOT:
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
45 bài tập Xác suất có lời giải
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận