Câu hỏi:
23/05/2022 1,882
Cho hàm số y=f(x) liên tục trên R, có 3 cực trị và có đồ thị như hình vẽ.
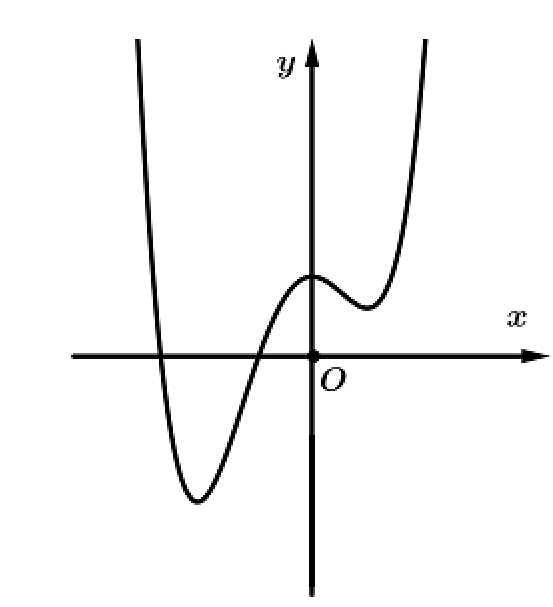
Tìm số điểm cực trị của hàm số y=f(1(x−1)2)
Cho hàm số y=f(x) liên tục trên R, có 3 cực trị và có đồ thị như hình vẽ.

Tìm số điểm cực trị của hàm số y=f(1(x−1)2)
Quảng cáo
Trả lời:
Phương pháp giải: Tính [(1(x−1)2)]′và tìm số nghiệm bội lẻ, từ đó suy ra số cực trị
Giải chi tiết:
Ta có:
g′(x)=[f(1(x−1)2)]′=[1(x−1)2]′.f′(1(x−1)2)=−2(x−1)3.f′(1(x−1)2)
g′(x)=0⇔f′(1(x−1)2)=0⇔[1(x−1)2=x1<0(VN)1(x−1)2=0(VN)1(x−1)2=x3>0
⇔x-1=±√1𝑥3⇔x=1±√1𝑥3 (nghiệm đơn)
Vậy hàm số đã cho có 2 điểm cực trị
Chọn D.
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Theo số liệu từ Tổng cục thống kê, dân số Việt Nam năm 2015 là 91,7 triệu người. Giả sử tỉ lệ tăng dân số hàng năm của Việt Nam trong giai đoạn 2015 – 2050 ở mức không đổi là 1,1%. Hỏi đến năm nào dân số Việt Nam sẽ đạt mức 120,5 triệu người?
Câu 2:
Một xe mô tô đang chạy với vận tốc 20m/s thì người lái xe nhìn thấy một chướng ngại vật nên đạp phanh. Từ thời điểm đó, mô tô chuyển động chậm dần đều với vận tốc v(t)=20−5t, trong đó t là thời gian (tính bằng giây) kể từ lúc đạp phanh. Quãng đường mà mô tô đi được từ khi người lái xe đạp phanh đến lúc mô tô dừng lại là
Câu 3:
Hai dao động điều hoà cùng phương, cùng tần số có biên độ và pha ban đầu lần lượt là A1, A2, φ1, φ2. Dao động tổng hợp của hai dao động trên có biên độ được tính theo công thức
Câu 4:
Mặt sàn của một thang máy có dạng hình vuông ABCD cạnh 2m được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ toạ độ Oxy với Olà tâm hình vuông sao choA(1;1) như hình vẽ bên thì các đường cong OA có phương trình y=x2 và y=ax3+bx. Tính giá trị ab biết rằng diện tích trang trí màu sẫm chiếm 13 diện tích mặt sàn.
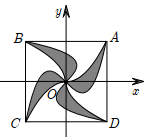

Câu 5:
Một chất điểm chuyển động theo quy luật S(t)=1+3t2−t3. Vận tốc của chuyển động đạt giá trị lớn nhất khi t bằng bao nhiêu?
Câu 6:
Tác phẩm nào sau đây KHÔNG thuộc về khuynh hướng văn học hiện thực?
Câu 7:
Cho a,blà các số nguyên và limx→1ax2+bx- 5x- 1= 20. Tính P=a2+b2−a−b.
Cho a,blà các số nguyên và limx→1ax2+bx- 5x- 1= 20. Tính P=a2+b2−a−b.

🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 8)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận