Câu hỏi:
24/05/2022 487Cho hàm số y=f(x) có đạo hàm liên tục trên và có bảng biến thiên như sau.
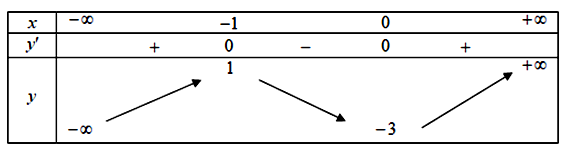
Hàm số y=f(x2−2x) nghịch biến trên khoảng nào dưới đây?
Đáp án chính xác
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Chọn f′(x)=x(x+1)
Khi đó g(x)=f(x2−2x)⇒g′(x)=(2x−2)f′(x2−2x)=(2x−2)(x2−2x)(x2−2x+1)
Ta có bảng xét dấu
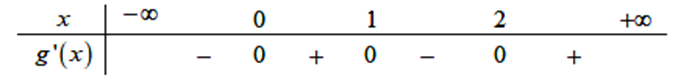
Do đó hàm số g(x) nghịch biến trên khoảng (1;2).
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;3),B(2;3;−4),C(−3;1;2). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
Xem đáp án »
24/05/2022
44,336
Câu 2:
Cho \2∫0f(x)dx=3 và 2∫0g(x)dx=7, khi đó 2∫0[f(x)+3g(x)]dx bằng
Xem đáp án »
24/05/2022
16,833
Câu 3:
Trong không gian với hệ tộa độ Oxyz, cho hai điểm A(0;1;−2) và B(3;−1;1). Tìm tọa độ của điểm M sao cho →AM=3→AB
Xem đáp án »
24/05/2022
16,168
Câu 5:
Cho hàm số y=f(x) có đạo hàm, nhận giá trị dương trên (0;+∞) và thỏa mãn 2f′(x2)=9x√f(x2) với mọi x∈(0;+∞). Biết f(23)=23, tính giá trị f(13).
Xem đáp án »
24/05/2022
6,502
Câu 6:
Trong không gian Oxyz, cho hai điểm A(−2;2;−2) và B(3;−3;3). Lấy M là điểm thay đổi luôn thỏa mãn MAMB=23. Giá trị lớn nhất của độ dài đoạn OM bằng
Xem đáp án »
24/05/2022
5,771
Câu 7:
Cho hàm số f(x) có đạo hàm f′(x) và thỏa mãn A=1∫0(2x+1)f', 3f\left( 1 \right) - f\left( 0 \right) = 12. Tính I = \int\limits_0^1 {f\left( x \right)d{\rm{x}}} .
Xem đáp án »
24/05/2022
5,466
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
45 bài tập Xác suất có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận