Cho hàm số y=f(x) có bảng biến thiên như sau

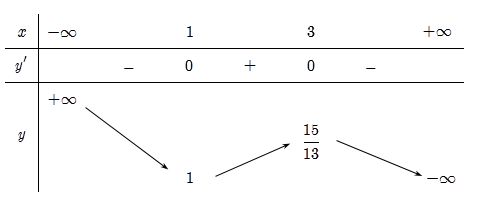
Biết f(0)=76, giá trị lớn nhất của mm để phương trình ${e^{2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}}} = m$ có nghiệm trên đoạn $\left[ {0;2} \right]\;$là

Ta có:

${e^{2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}}} = m \Leftrightarrow 2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2} = \ln m$

Xét $g\left( x \right) = 2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}$có:

$g'\left( x \right) = 6{f^2}\left( x \right)f'\left( x \right) - 13f\left( x \right)f'\left( x \right) + 7f'\left( x \right) = f'\left( x \right)\left[ {6{f^2}\left( x \right) - 13f\left( x \right) + 7} \right]$

Suy ra

$g\prime (x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{f\prime (x) = 0}\\{6{f^2}(x) - 13f(x) + 7 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{f\prime (x) = 0}\\{f(x) = 1}\\{f(x) = \frac{7}{6}}\end{array}} \right.$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1;x = 3}\\{x = 1,x = {x_1} > 3}\\{x = {x_2} < 1}\end{array}} \right.$

Xét g(x) trên đoạn $[0;2].$

+ Trong khoảng (0;1) thì$f'\left( x \right) < 0,f\left( x \right) > 1,f\left( x \right) < f(0) = \frac{7}{6}$nên$f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \frac{7}{6}} \right) > 0$hay$g'\left( x \right) > 0$</></>

+ Trong khoảng (1;2) thì $f'\left( x \right) > 0,f\left( x \right) > 1,f\left( x \right) < \frac{{15}}{{13}} < \frac{7}{6}$nên$f'\left( x \right)\left( {f\left( x \right) - 1} \right)\left( {f\left( x \right) - \frac{7}{6}} \right) < 0$hay $g'\left( x \right) < 0$

Từ đó ta có bảng biến thiên của g(x) như sau:

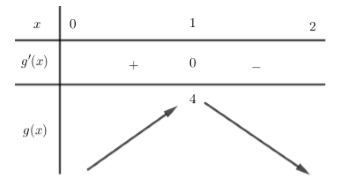
Từ bảng biến thiên ta thấy $\mathop {\max }\limits_{\left[ {0;2} \right]} g\left( x \right) = 4$

Vậy yêu cầu bài toán thỏa nếu và chỉ nếu$\ln m \le 4 \Leftrightarrow m \le {e^4}$hay giá trị lớn nhất của m là $m = {e^4}$.

Đáp án cần chọn là: A