Có bao nhiêu số nguyên [a in left( { - 2019;2019} right) ] để phương trình [ frac{1}{{ ln left( {x + 5} right)}} + frac{1}{{{3^x} - 1}} = x + a ] có hai nghiệm phân biệt? A.0 B.2022 C.2014 D.2015

[ frac{1}{{ ln left( {x + 5} right)}} + frac{1}{{{3^x} - 1}} = x + a Leftrightarrow f left( x right) = frac{1}{{ ln left( {x + 5} right)}} + frac{1}{{{3^x} - 1}} - x = a , , left( * right) ] Xét hàm số [f left( x right) = frac{1}{{ ln left( {x + 5} right)}} + frac{1}{{{3^x} - 1}} - x ] ĐKXĐ: ( left { { begin{array}{*{20}{c}}{x + 5 > 0} { begin{array}{*{20}{c}}{ln(x + 5) ne 0} {{3^x} - 1 ne 0} end{array}} end{array}} right. Leftrightarrow left { { begin{array}{*{20}{c}}{x > - 5} {x + 5 ne 1} {{3^x} ne 1} end{array}} right. Leftrightarrow left { { begin{array}{*{20}{c}}{x > - 5} {x ne - 4} {x ne 0} end{array}} right. 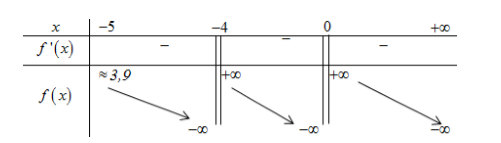) [ Rightarrow D = left( { - 5; - 4} right) cup left( { - 4;0} right) cup left( {0; + infty } right) ] Ta có: [f' left( x right) = - frac{1}{{ left( {x + 5} right){{ ln }^2} left( {x + 5} right)}} - frac{{{3^x} ln 3}}{{{{ left( {{3^x} - 1} right)}^2}}} - 1 < 0, forall x in D ] BBT: Từ BBT suy ra phương trình (*) có 2 nghiệm [ Leftrightarrow a ge 4 ] Kết hợp ĐK [ Rightarrow a in left { {4;...;2018} right } ]Vậy có 2015 giá trị của a thỏa mãn. Đáp án cần chọn là: D

Có bao nhiêu số nguyên

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Siêu tiết kiệm - Được thi tất cả các đề của các lớp có trên Khoahoc.vietjack.com
Ngân hàng câu hỏi trắc nghiệm theo các mức độ Nhận biết, Thông hiểu, Vận dụng, Vận dụng cao.
Luyện chuyên sâu, rèn tốc độ với trọn bộ đề thi thử, đề minh họa, chính thức các năm.
Hỏi bài tập với đội ngũ chuyên môn cao của chúng tôi.

Đặt mua

Có bao nhiêu số nguyên $a \in \left( { - 2019;2019} \right)$ để phương trình $\frac{1}{{\ln \left( {x + 5} \right)}} + \frac{1}{{{3^x} - 1}} = x + a$ có hai nghiệm phân biệt?