Câu hỏi:
27/06/2022 311Cho hàm số y=f(x) liên tục trên R và có đạo hàm f′(x)=x2(x−2)(x2−6x+m) với mọi x∈R. Có bao nhiêu số nguyên m thuộc đoạn [−2019;2019] để hàm số g(x)=f(1−x) nghịch biến trên khoảng (−∞;−1)?
Đáp án chính xác
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Để g(x) nghịch biến trên (−∞;−1) thì g′(x)≤0∀x∈(−∞;−1)
⇔f′(1−x)(1−x)′≤0∀x∈(−∞;−1)
⇔−(1−x2)(−1−x)(x2+4x+m−5)≤0∀x∈(−∞;−1)
⇔(x+1)(x2+4x+m−5)≤0∀x∈(−∞;−1)
⇔(x2+4x+m−5)≥0∀x∈(−∞;−1)
⇔m≥−x2−4x+5∀x∈(−∞;−1)
⇔m≥max
\Leftrightarrow m \ge 9
Do m thuộc đoạn \left[ { - 2019;2019} \right] và m nhận giá trị nguyên nên sẽ có 2011 giá trị.
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số f\left( x \right) liên tục trên \mathbb{R} và \int\limits_0^6 {f\left( x \right)d{\rm{x}}} = 10, thì \int\limits_0^3 {f\left( {2{\rm{x}}} \right)d{\rm{x}}} bằng
Xem đáp án »
27/06/2022
13,144
Câu 2:
Cho đồ thị hàm số y = f\left( x \right) như hình vẽ bên. Diện tích phần hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right) với trục Ox nằm phía trên và phía dưới trục Ox lần lượt là 3 và 1. Khi đó \int\limits_{ - 2}^3 {f\left( x \right)d{\rm{x}}} bằng
Xem đáp án »
27/06/2022
9,399
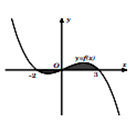
Câu 3:
Cho 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 10 điểm trên?
Xem đáp án »
27/06/2022
5,175
Câu 4:
Trong không gian Oxyz, mặt phẳng \left( P \right) đi qua điểm A\left( {1;0;2} \right) và vuông góc với đường thẳng d:\frac{x}{2} = \frac{{y - 1}}{{ - 1}} = \frac{{z + 2}}{3} có phương trình là
Xem đáp án »
27/06/2022
4,812
Câu 5:
Số nghiệm nguyên của bất phương trình {\log _{\frac{1}{2}}}\left( {x - 3} \right) \ge {\log _{\frac{1}{2}}}4 là
Xem đáp án »
27/06/2022
3,046
Câu 6:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng \sqrt 2 a. Độ lớn của góc giữa đường thẳng SA và mặt phẳng đáy bằng
Xem đáp án »
27/06/2022
2,732
Câu 7:
Cho hàm số f\left( x \right) = \frac{{\ln \left( {{x^2} + 1} \right)}}{x} thỏa mãn f'\left( 1 \right) = a\ln 2 + b với a,b \in \mathbb{Z}. Giá trị của a + b bằng
Xem đáp án »
27/06/2022
2,608
🔥 Đề thi HOT:
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
45 bài tập Xác suất có lời giải
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận