Câu hỏi:
05/07/2022 1,780Cho hàm số y=f(x)y=f(x) có đạo hàm f′(x)=x(x−1)2(3x4+mx3+1) với mọi x∈R. Có bao nhiêu số nguyên âm m để hàm số g(x)=f(x2) đồng biến trên khoảng (0;+∞)?
Đáp án chính xác
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Ta có: g′(x)=2x.f′(x2)=2x.x4.(x2−1)2.(3x8+mx6+1)
Hàm số g(x)=f(x2) đồng biến trên khoảng (0;+∞)⇔g′(x)≥0(∀x∈(0;+∞))
⇔3x8+mx6+1≥0∀x∈(0;+∞)⇔h(x)=3x2+1x6+m≥0∀x∈(0;+∞)
⇔Min(0;+∞)h(x)≥0 (*)
Mặt khác với x∈(0;+∞) thì 3x2+1x6=x2+x2+x2+1x6≥44√x2.x2.x2.1x6=4
Do đó (*) ⇔4+m≥0⇔m≥−4
Kết hợp m∈+⇒m={−4;−3;−2;−1}.
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tính diện tích S của phần hình phẳng gạch sọc (như hình vẽ bên dưới) giới hạn bởi đồ thị của hàm số bậc ba y=ax3+bx2+cx+d và trục hoành.
Xem đáp án »
05/07/2022
5,397
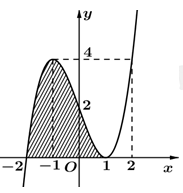
Câu 3:
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=x3−3x2+4 trên đoạn [−1;3]. Giá trị của biểu thức P=M2−m2 là
Xem đáp án »
05/07/2022
3,338
Câu 4:
Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình hình chiếu của đường thẳng d:x+32=y+11=z−1 trên mặt phẳng (P):x−3y+2z+6=0?
Xem đáp án »
05/07/2022
2,332
Câu 5:
Một hình trụ có bán kính đáy và chiều cao đều bằng 4 dm. Một hình vuông ABCD có hai cạnh AB và CD lần lượt là các dây cung của hai đường tròn đáy. Biết mặt phẳng (ABCD) không vuông góc với mặt đáy của hình trụ. Tính diện tích S của hình vuông ABCD.
Xem đáp án »
05/07/2022
2,185
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P):x+y−z−2=0, (Q):x+3y−12=0 đường thẳng d:x−13=y+2−1=z+12. Viết phương trình mặt phẳng (R) chứa đường thẳng d và giao tuyến của hai mặt phẳng (P),(Q).
Xem đáp án »
05/07/2022
2,152
Câu 7:
Cho hàm số y=f(x). Hàm số y=f′(x) có đồ thị như hình vẽ bên. Bất phương trình 3f(x)+x3<a−3xlnx có nghiệm thuộc đoạn [1;2] khi và chỉ khi
Xem đáp án »
05/07/2022
1,890
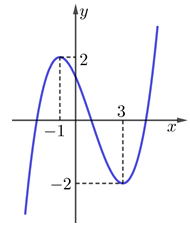
🔥 Đề thi HOT:
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
45 bài tập Xác suất có lời giải
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận