Câu hỏi:
12/07/2024 211
Cho tam giác nhọn DEF,DEF, hai đường cao EM,FNEM,FN cắt nhau tại I
a) Chứng minh hai tam giác DMEDME và DNFDNF đồng dạng
b) Chứng minh IM.IE=IN.IFIM.IE=IN.IF
c) Cho biết ^EDF=450.ˆEDF=450. Chứng tỏ rằng: (MNEF)2=12(MNEF)2=12
Cho tam giác nhọn DEF,DEF, hai đường cao EM,FNEM,FN cắt nhau tại I
a) Chứng minh hai tam giác DMEDME và DNFDNF đồng dạng
b) Chứng minh IM.IE=IN.IFIM.IE=IN.IF
c) Cho biết ^EDF=450.ˆEDF=450. Chứng tỏ rằng: (MNEF)2=12(MNEF)2=12
Câu hỏi trong đề:
Bài tập theo tuần Toán 8 - Tuần 35 !!
Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 49k/cuốn).
Quảng cáo
Trả lời:
Giải bởi Vietjack
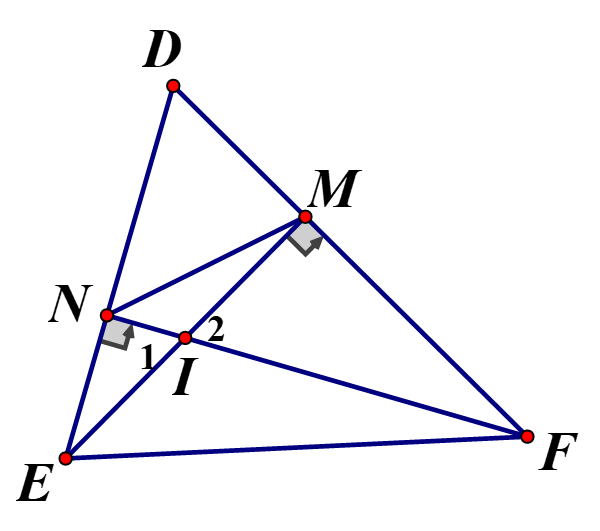
a) Xét ΔDMEΔDME và ΔDNFΔDNF có: ˆDˆD chung; ⇒ΔDME~ΔDNF(g−g)⇒ΔDME~ΔDNF(g−g)
b) Xét ΔINEΔINE và ΔIMFΔIMF có: ^I1=^I2ˆI1=ˆI2 (đối đỉnh); ˆN=ˆM=900ˆN=ˆM=900⇒ΔINE~ΔIMF(g−g)⇒ΔINE~ΔIMF(g−g)
(các cặp cạnh tương ứng tỉ lệ)
c) Vì ΔDME~ΔDNF(cmt)⇒DMDE=DNDFΔDME~ΔDNF(cmt)⇒DMDE=DNDF
Xét ΔNDMΔNDM và ΔFDEΔFDE có: DMDE=DNDFDMDE=DNDF (cmt); góc D chung
Mặt khác ΔDMEΔDME vuông tại M có ˆD=450⇒ΔDMEˆD=450⇒ΔDME vuông cân ⇒DMDE=1√2(2)⇒DMDE=1√2(2)
Từ (1) và (2) suy ra MNEF=1√2⇒(MNEF)2=12MNEF=1√2⇒(MNEF)2=12
Nhà sách VIETJACK:
Sách - Sổ tay Toán 8 (Takenote) cho cả 3 bộ Kết nối tri thức, Chân trời sáng tạo, Cánh diều VietJack
Đã bán 212
₫ 60.000
₫ 30.000
Trọng tâm Toán, Anh, KHTN lớp 8 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025
Đã bán 374
₫ 130.000
₫ 60.000
Combo 2 sách Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 8 cho cả 3 bộ KNTT; CTST; CD VietJack
Đã bán 287
₫ 230.000
₫ 120.000
Combo 2 sách Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 cho cả 3 bộ KNTT; CTST; CD VietJack
Đã bán 361
₫ 245.000
₫ 126.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số 4x-1<8
Xem đáp án »
12/07/2024
1,993
Câu 5:
Tổ chức từ thiện đang quyên góp nhằm ủng hộ 5000 đồng bào bị bão lụt. Hiếu quyết định ủng hộ x%x% số tiền mình đang có (x<100).(x<100). Biểu thức nào sau đây biểu thị số tiền Hiếu còn lại để đi mua bánh ?
Xem đáp án »
02/08/2022
697
Câu 7:
Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số 4x-1<8
Xem đáp án »
12/07/2024
509
🔥 Đề thi HOT:
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận