10 Bài tập Chứng minh các hệ thức hình học (có lời giải)
63 người thi tuần này 4.6 485 lượt thi 10 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 08
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 07
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 06
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 05
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 04
Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
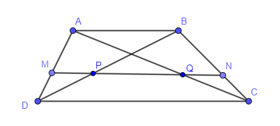
Xét tam giác ADB có MP // AB nên theo định lí Thalès ta có:
(1)
Xét tam giác CDB có NP // DC nên theo định lí Thalès ta có:
(2)
Từ (1) và (2) suy ra .
Câu 2
Lời giải
Đáp án đúng là: A
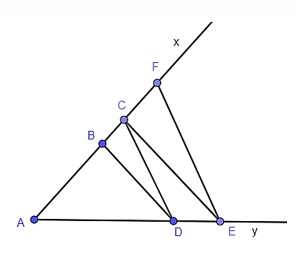
Xét tam giác ACE có CE // BD nên theo định lí Thalès ta có:
(1)
Xét tam giác AFE có FE // CD nên theo định lí Thalès ta có:
(2)
Từ (1) và (2) suy ra .
Từ đó ta có AC ⋅ AC = AB ⋅ AF hay AC2 = AB ⋅ AF.
Câu 3
A.
B.
C.
D. DE // BC.
Lời giải
Đáp án đúng là: C
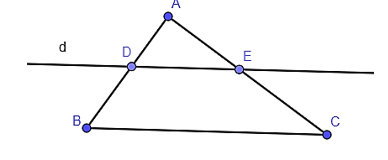
Trong tam giác ABC có nên DE // BC (định lí Thalès đảo).
Do đó theo định lí Thalès ta có , .
Vậy C sai.
Lời giải
Đáp án đúng là: C
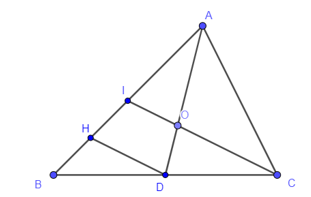
Kẻ DH // CI (H ∈ AB), do đó DH // IO.
Xét tam giác ADH có DH // IO nên theo định lí Thalès ta có:
hay .
Suy ra AI = 3t và IH = 2t (với t > 0).
Ta có D thuộc cạnh BC và BC = 2BD, suy ra BC = 2CD.
Xét tam giác BIC có DH // IC nên theo định lí Thalès ta có:
hay
Suy ra BI = 2IH = 2 ⋅ 2t = 4t.
Vậy .
Lời giải
Đáp án đúng là: D
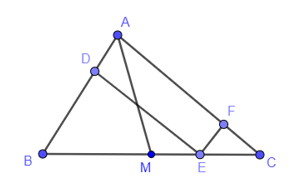
Xét tứ giác ADEF có:
AD // EF (D ∈ AB)
AF // DE (F ∈ AC)
Suy ra tứ giác ADEF là hình bình hành.
Do đó AF = DE (1).
Xét tam giác ABC có EF // AB nên theo định lí Thalès ta có:
(2)
Từ (1) và (2) suy ra .
Câu 6
D. Cả A, B đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.