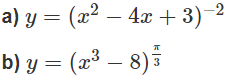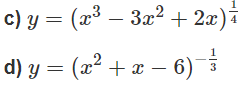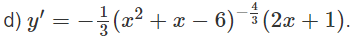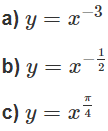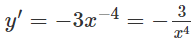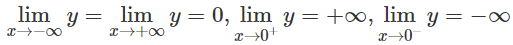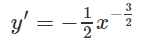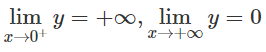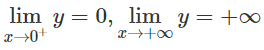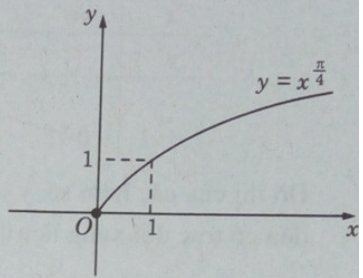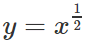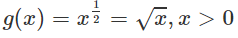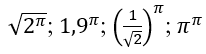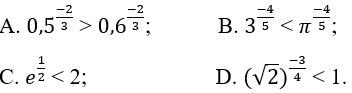Giải sbt Giải tích 12 Bài 2: Hàm số lũy thừa
34 người thi tuần này 4.6 1.7 K lượt thi 9 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 3
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 2
Đề kiểm tra Phương pháp tọa độ trong không gian (có lời giải) - Đề 1
Đề kiểm tra Ứng dụng hình học của tích phân (có lời giải) - Đề 3
Đề kiểm tra Ứng dụng hình học của tích phân (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
a) Hàm số xác định khi − 4x + 3 ≠ 0 hay x ≠ 1; x ≠ 3.
Vậy tập xác định của hàm số đã cho là R \ {1;3}.
b) Hàm số xác định khi – 8 > 0 hay x > 2. Vậy tập xác định là (2; +).
c) Hàm số xác định khi – 3 + 2x > 0 hay x(x – 1)(x – 2) > 0
Lời giải
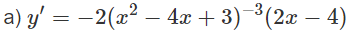
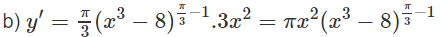
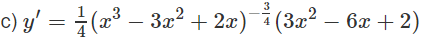
Lời giải
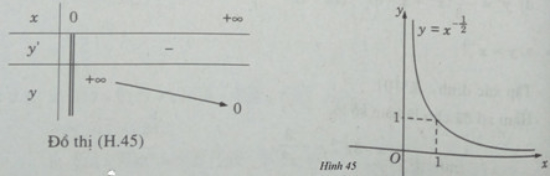
a) Tập xác định: R\{0}
Hàm số đã cho là hàm số lẻ.
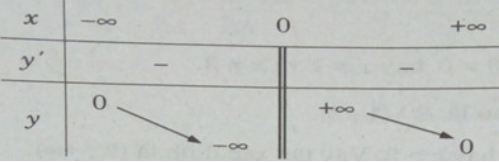
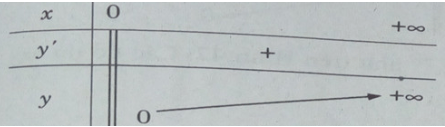
Ta có: y′ < 0, ∀ x ∈ R \ {0} nên hàm số luôn nghịch biến trên các khoảng xác định.
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
Bảng biến thiên:
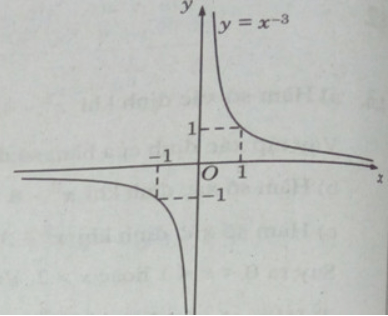
Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.
b) Tập xác định: D = (0; +∞)
Vì y' < 0 ∀ x ∈ D nên hàm số nghịch biến.
Đồ thị có tiệm cận đứng là trục tung, tiệm cận ngang là trục hoành.
Bảng biến thiên:
c) Tập xác định: D = (0; +)
y′ > 0, ∀ x ∈ D
Vì y′ > 0, ∀ x ∈ D nên hàm số nghịch biến.
Đồ thị không có tiệm cận.
Bảng biến thiên
Đồ thị
Lời giải
Đặt f(x) = , x ∈ R
Đồ thị:
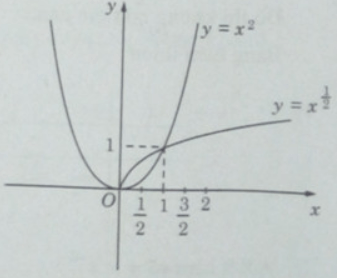
Từ đồ thị của hai hình đó ta có:
f(0,5) < g(0,5);
f(1) = g(1) = 1;
f(3/2) > g(3/2), f(2) > g(2);
f(3) > g(3), f(4) > g(4).
Lời giải
Đáp án: C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.