10 bài tập Giải toán tam giác liên quan đến tỉ lệ cạnh đáy - chiều cao có lời giải
71 người thi tuần này 4.6 158 lượt thi 10 câu hỏi 45 phút
🔥 Đề thi HOT:
Bài tập cuối tuần Toán lớp 5 KNTT Tuần 12 có đáp án
Bài tập cuối tuần Toán lớp 5 KNTT Tuần 13 có đáp án
15 câu trắc nghiệm Toán lớp 5 Kết nối tri thức Ôn tập số tự nhiên có đáp án
Bài tập cuối tuần Toán lớp 5 KNTT Tuần 10 có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
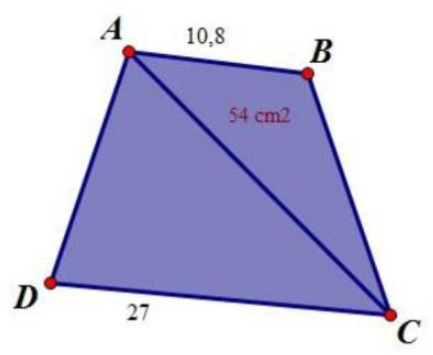
Chiều cao của tam giác ABC (hạ từ đỉnh C) cũng bằng chiều cao của hình thang và bằng chiều cao hạ từ A của tam giác ADC và nó bằng:
\(2 \times 54:10,8 = 10{\rm{ (cm)}}\)
Diện tích tam giác ADC là: \(27 \times 10:2 = 135{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Đáp Số: \(135{\rm{ c}}{{\rm{m}}^2}\).
Lời giải
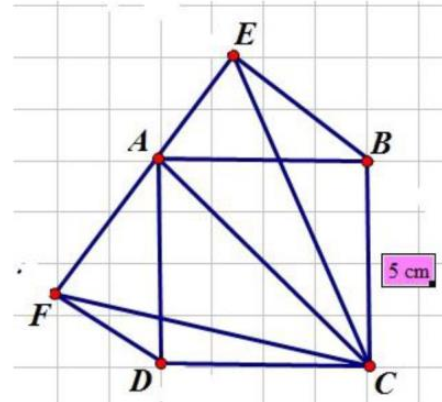
Ta có: \(S.ABCD = 5 \times 5 = 25{\rm{ c}}{{\rm{m}}^2}\)
Do EB // AC nên tứ giác EBCA là hình thang. Do đó, đường cao hạ từ E và B xuống AC là bằng nhau và bằng chiều cao hình thang EBCA.
Vậy \(S.EAC = S.BAC\) (do chiều cao bằng nhau và chung đáy AC)
Mà \(S.BAC = 25:2 = 12,5{\rm{ c}}{{\rm{m}}^2}\).
Tương tự, ta cũng sẽ có được FECA là hình thang.
Và \(S.FAC = S.DAC = 12,5{\rm{ c}}{{\rm{m}}^2}\)
Mà \(S.CEF = S.EAC + S.FAC = 12,5 + 12,5 = 25{\rm{ c}}{{\rm{m}}^2}\)
Vậy \(S.CEF = 25{\rm{ c}}{{\rm{m}}^2}\).
Đáp Số: \(25{\rm{ c}}{{\rm{m}}^2}\).
Lời giải
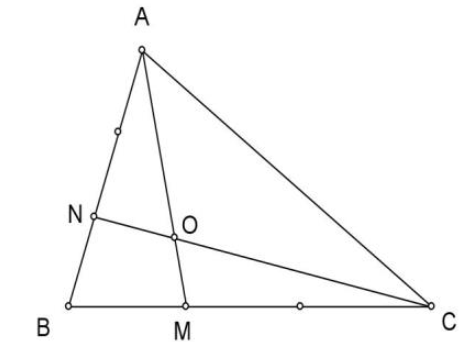
\({S_{OBN}} = \frac{1}{2}{S_{OAN}} = 4{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
\({S_{OAC}} = 2{S_{OAB}} = 2 \times 12 = 24{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Ta có: \({S_{OMC}} = 2{S_{OBM}}\) và \({S_{OAC}} = 2{S_{OBC}}\)
\( \Rightarrow {S_{OAC}} = 2 \times ({S_{OMC}} + {S_{OBM}}) = 2 \times (2 \times {S_{OBM}} + {S_{OBM}}) = 6 \times {S_{OBM}}\)
\( \Rightarrow {S_{OBM}} = 24:6 = 4{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Vậy \({S_{BNOM}} = 4 + 4 = 8{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Đáp Số: \(8{\rm{ c}}{{\rm{m}}^2}\)
Lời giải
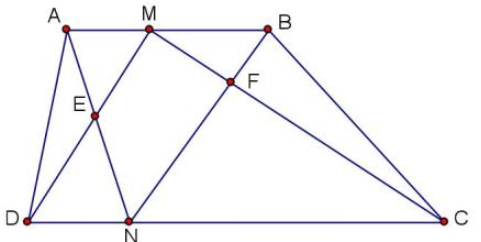
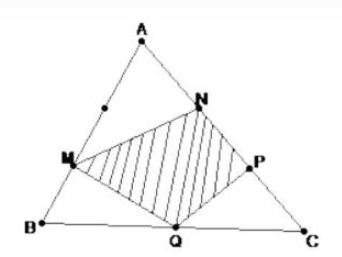
Ta có: \({S_{ADN}} = {S_{MDN}}\) (cùng đáy DN và có chiều cao bằng nhau)
\( \Rightarrow {S_{AED}} + {S_{EDN}} = {S_{MEN}} + {S_{EDN}} \Rightarrow {S_{ADE}} = {S_{MEN}} \Rightarrow {S_{MEN}} = 2{\rm{ c}}{{\rm{m}}^2}\)
Tương tự cũng có: \({S_{MCN}} = {S_{BCN}}\)
\( \Rightarrow {S_{MFN}} + {S_{FCN}} = {S_{BFC}} + {S_{FCN}} \Rightarrow {S_{MFN}} = {S_{BFC}} \Rightarrow {S_{MFN}} = 3{\rm{ c}}{{\rm{m}}^2}\)
Mà: \({S_{MENF}} = {S_{MEN}} + {S_{MFN}} \Rightarrow {S_{MEFN}} = 2 + 3 = 5{\rm{ c}}{{\rm{m}}^2}\)
Đáp Số: \(5{\rm{ c}}{{\rm{m}}^2}\)
Lời giải
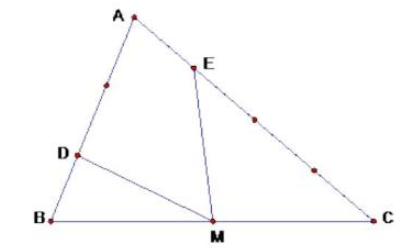
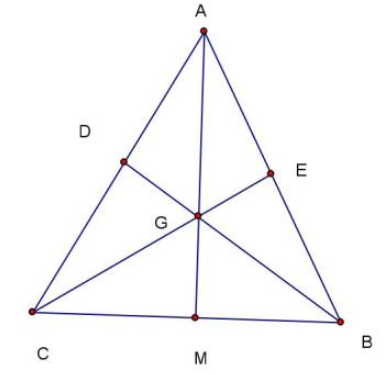
\({S_{MDB}} = \frac{1}{3} \times {S_{ABM}} = \frac{1}{3} \times \frac{1}{2} \times {S_{ABC}} = 3{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
\({S_{MCE}} = \frac{3}{4} \times {S_{ACM}} = \frac{3}{4} \times \frac{1}{2} \times {S_{ABC}} = 6,75{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Do đó: \({S_{MDB}} + {S_{MCE}} = 3 + 6,75 = 9,75{\rm{ (c}}{{\rm{m}}^2}{\rm{)}}\)
Đáp Số: \(9,75{\rm{ c}}{{\rm{m}}^2}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.