Bài tập Định lí có đáp án
47 người thi tuần này 4.6 1.1 K lượt thi 8 câu hỏi
🔥 Đề thi HOT:
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
20.4 K lượt thi
17 câu hỏi
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
7.2 K lượt thi
30 câu hỏi
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
15 K lượt thi
15 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
15.7 K lượt thi
17 câu hỏi
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
5.6 K lượt thi
23 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
15.4 K lượt thi
29 câu hỏi
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
5.6 K lượt thi
21 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 4
15 K lượt thi
29 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
Bạn Ánh vẽ hai đường thẳng a, b song song với nhau và khẳng định với bạn Ngân rằng: “Nếu đường thẳng c cắt hai đường thẳng song song đó thì hai góc so le trong bằng nhau” (Hình 48).
Câu khẳng định có dạng “Nếu … thì …” trong toán học được gọi là gì?
Câu khẳng định có dạng “Nếu … thì …” trong toán học được gọi là gì?
Lời giải
Để trả lời được câu hỏi này, ta đi tìm hiểu mục Kiến thức trọng tâm của mục I trang 106.
Câu 2
Đọc kĩ nội dung sau.
Cho hai góc kề bù là xOy và yOz, Om và On lần lượt là tia phân giác của góc xOy và góc yOz (Hình 49).
Ta thấy và , suy ra:
.
Như vậy, có thể khẳng định: “Nếu một góc có hai cạnh là hai tia phân giác của hai góc kề bù thì đó là góc vuông”.
Đọc kĩ nội dung sau.
Cho hai góc kề bù là xOy và yOz, Om và On lần lượt là tia phân giác của góc xOy và góc yOz (Hình 49).
Ta thấy và , suy ra:
.
Như vậy, có thể khẳng định: “Nếu một góc có hai cạnh là hai tia phân giác của hai góc kề bù thì đó là góc vuông”.
Lời giải
Học sinh đọc kĩ các nội dung của hoạt động.
Câu 3
Xét khẳng định “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau”, ta thấy: Khẳng định này được phát biểu ở dạng “Nếu … thì …”. Trong khẳng định đó, hãy nêu:
- Phần nằm giữa hai từ “Nếu” và từ “thì”;
- Phần nằm sau từ “thì”.
Xét khẳng định “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau”, ta thấy: Khẳng định này được phát biểu ở dạng “Nếu … thì …”. Trong khẳng định đó, hãy nêu:
- Phần nằm giữa hai từ “Nếu” và từ “thì”;
- Phần nằm sau từ “thì”.
Lời giải
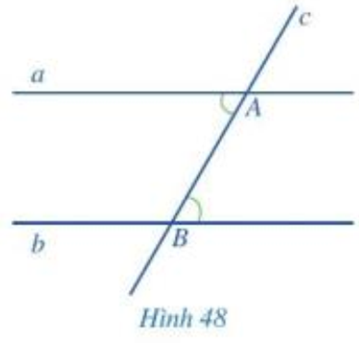
- Phần nằm giữa hai từ “Nếu” và từ “thì” là “một đường thẳng cắt hai đường thẳng song song”;
- Phần nằm sau từ “thì” là “hai góc so le trong bằng nhau”.
Câu 4
Nêu giả thiết và kết luận của định lý: “Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b song song với nhau”.
Nêu giả thiết và kết luận của định lý: “Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b song song với nhau”.
Lời giải
- Giả thiết: một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau.
- Kết luận: hai đường thẳng a, b song song với nhau.
Câu 5
Cho định lí:
“Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết và kết luận của định lí trên.
c) Chứng tỏ định lí trên là đúng.
Cho định lí:
“Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết và kết luận của định lí trên.
c) Chứng tỏ định lí trên là đúng.
Lời giải
a) Giả sử hai đường thẳng xx’ và yy’ cắt nhau tại điểm O.
Khi đó, hai góc xOy và góc x’Oy’ là hai góc đối đỉnh.
Ta có hình vẽ sau:
b) Giả thiết và kết luận của định lí:
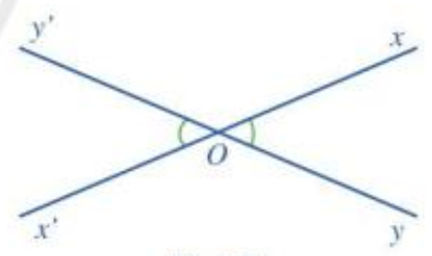
- Giả thiết: Hai góc xOy và x’Oy’ là hai góc đối đỉnh.
- Kết luận: .
c) Do góc xOy và góc x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau.
Suy ra và là hai góc kề bù nên:
(1)
Tương tự, ta có:
(2)
Từ (1) và (2) ta suy ra: .
Vậy .
Câu 6
Chứng minh định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau.
Chứng minh định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau.
Lời giải
Giả sử hai đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại hai điểm A và B.
Ta có: (hai góc đối đỉnh)
(GT)
Suy ra (cùng bằng ).
Tương tự, ta chứng minh được các cặp gócCâu 7
Vẽ hình minh họa và viết giả thiết, kết luận bằng kí hiệu cho mỗi định lí sau:
a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
b) Hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì chúng song song với nhau.
c) Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với một đường thẳng cho trước.
Vẽ hình minh họa và viết giả thiết, kết luận bằng kí hiệu cho mỗi định lí sau:
a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
b) Hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì chúng song song với nhau.
c) Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với một đường thẳng cho trước.
Lời giải
a) Định lí “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
b) Định lí “Hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì chúng song song với nhau”.
c) Định lí “Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với một đường thẳng cho trước”.
Câu 8
Cho định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì song song với nhau”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết, kết luận của định lí trên.
c) Chứng minh định lí trên.
Cho định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì song song với nhau”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết, kết luận của định lí trên.
c) Chứng minh định lí trên.
Lời giải
Định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì song song với nhau”.
a) Ta có hình vẽ:
b) Giả thiết, kết luận của định lí:
c) Chứng minh định lí:
Ta có: tại A nên ;
tại B nên .
Khi đó, .
Mà và ở vị trí đồng vị.
Do đó a // b.
4.6
226 Đánh giá
50%
40%
0%
0%
0%