Giải VBT Toán 7 Cánh diều Bài 3. Hai tam giác bằng nhau có đáp án

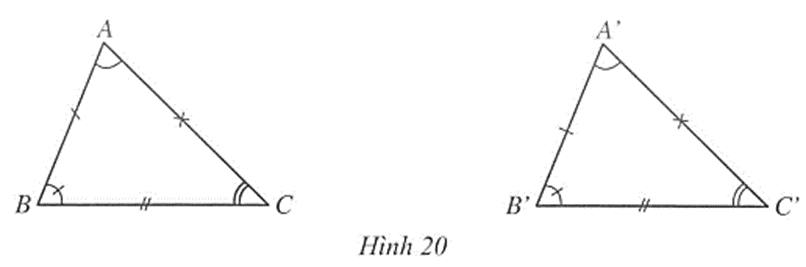
- Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

- Khi hai tam giác ABC và A’B’C’ bằng nhau thì ta kí hiệu là: ∆ABC = ∆A’B’C’.

+ Nếu AB = A’B’, BC = B’C’, CA = C’A’ và \(\widehat A\)= \(\widehat {A'}\), \(\widehat B\)= \(\widehat {B'}\), \(\widehat C\)= \(\widehat {C'}\) thì ∆ABC = ∆A’B’C’.

+ Nếu ∆ABC = ∆A’B’C’ thì AB = A’B’, BC = B’C’, CA = C’A’ và \(\widehat A\)= \(\widehat {A'}\), \(\widehat B\)= \(\widehat {B'}\), \(\widehat C\)= \(\widehat {C'}\).

Vì ∆ABC = ∆MNP nên

AC = MP (hai cạnh tương ứng); \(\widehat {ACB}\)= \(\widehat {MPN}\)(hai góc tương ứng)

Mà AC = 4 cm và \(\widehat {MPN}\)= 45^o nên MP = 4 cm, \(\widehat {ACB}\) = 45^o.

Vì ∆ABC = ∆DEG nên AB = DE, BC = EG, CA = GD

Ta có: \(\widehat P\) + \(\widehat Q\) + \(\widehat R\) = 180^o (tổng ba góc của một tam giác), \(\widehat P\)= 71^o, \(\widehat Q\)= 49^o.

Suy ra: \(\widehat R\) = 180^o – (\(\widehat P\) + \(\widehat Q\)) = 180^o – (71^o + 49^o) = 60^o

Do ∆PQR = ∆IHK nên \(\widehat R\) = \(\widehat K\) (hai góc tương ứng). Suy ra \(\widehat K\) = 60^o.

Vì ∆ABC = ∆MNP nên \(\widehat A\) = \(\widehat M\)( hai góc tương ứng)

Do \(\widehat A\) + \(\widehat N\) = \(\widehat M\) + \(\widehat N\) Mà \(\widehat A\) + \(\widehat N\) = 125^o nên \(\widehat M\) + \(\widehat N\) = 125^o.

Ta có \(\widehat M\) + \(\widehat N\) + \(\widehat P\) = 180^o (tổng ba góc của một tam giác)

Suy ra 125^o + \(\widehat P\) = 180^o vì thế \(\widehat P\) = 180^o – 125^o = 55^o.

Vì ∆AMB = ∆AMC nên: MB = MC (hai cạnh tương ứng);

\(\widehat {BAM}\) = \(\widehat {CAM}\), \(\widehat {AMB}\) = \(\widehat {AMC}\) (hai góc tương ứng)

Do tia AM nằm trong góc BAC và \(\widehat {BAM}\) = \(\widehat {CAM}\) nên tia AM là tia phân giác của góc BAC

Ta có \(\widehat {AMB}\) + \(\widehat {AMC}\) = 180^o (hai góc kề bù) và \(\widehat {AMB}\) = \(\widehat {AMC}\) nên \(\widehat {AMB}\) = \(\widehat {AMC}\) = 90^o.

Vậy AM \( \bot \) BC.

Ta có ∆OAB = ∆OCD nên \(\widehat {OAB}\) = \(\widehat {OCD}\)

Lại có \(\widehat {OAB}\) và \(\widehat {OCD}\) là hai góc so le trong

Suy ra a // b.