10 Bài tập Nhận biết tia, hai tia đối nhau (có lời giải)
63 người thi tuần này 4.6 359 lượt thi 10 câu hỏi 60 phút
🔥 Đề thi HOT:
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
25.9 K lượt thi
11 câu hỏi
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
12.7 K lượt thi
40 câu hỏi
Dạng 4: Trung điểm của đoạn thẳng có đáp án
7.7 K lượt thi
57 câu hỏi
Dạng 4: Một số bài tập nâng cao về lũy thừa
13.8 K lượt thi
10 câu hỏi
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
11.5 K lượt thi
31 câu hỏi
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 2)
9.4 K lượt thi
13 câu hỏi
Đề thi cuối học kỳ 2 Toán 6 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
2.1 K lượt thi
29 câu hỏi
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 2
22.5 K lượt thi
11 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
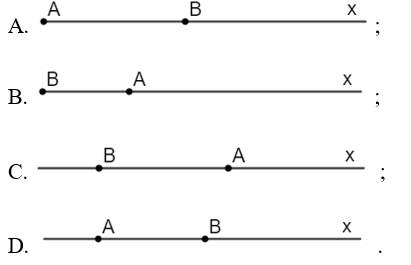
Đáp án đúng là: C
Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.
Lời giải
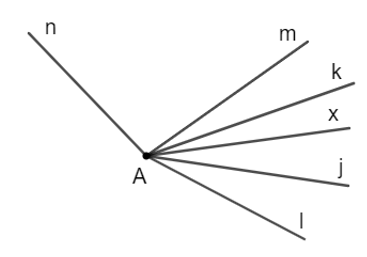
Đáp án đúng là: D
Khi đọc (viết) tên một tia, phải đọc (viết) tên gốc trước.
Các tia có trong hình vẽ trên là: An, Am, Ak, Ax, Aj, Al.
Lời giải
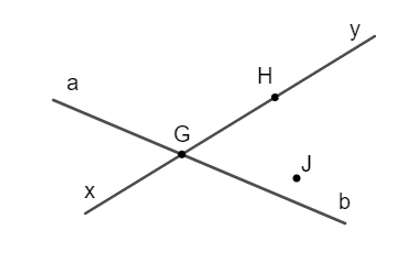
Đáp án đúng là: C
Điểm nằm trên đường thẳng ab là G nên có các tia là: Ga, Gb.
Các điểm nằm trên đường thẳng xy là: G và H nên có các tia là: Gx, GH, Gy, Hx, HG, Hy.
Điểm J không thuộc đường thẳng nào nên k có tia gốc J.
Vậy có tất cả 8 tia.
Lời giải
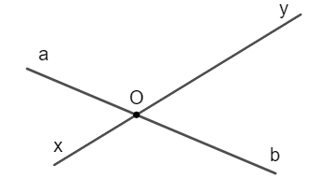
Đáp án đúng là: C
Hai đường thẳng ab và xy cắt nhau tại điểm O tạo thành 4 tia gốc O là: Oa, Ob, Ox, Oy.
Lời giải
Đáp án đúng là: D
• Hai tia Aa và AB là hai tia chung gốc nhưng không tạo thành một đường thẳng nên không phải là hai tia đối nhau.
• Hai tia BA và Bb là hai tia chung gốc nhưng không tạo thành một đường thẳng nên không phải là hai tia đối nhau.
• Hai tia BA và AB không chung gốc nên không phải là hai tia đối nhau.
• Hai tia Ba và Bb là hai tia chung gốc và tạo thành một đường thẳng nên là hai tia đối nhau.
Câu 6
Chọn cụm từ thích hợp để điền vào chỗ trống.
“Điểm I bất kỳ nằm trên đường thẳng xy là gốc chung của ….”
Chọn cụm từ thích hợp để điền vào chỗ trống.
“Điểm I bất kỳ nằm trên đường thẳng xy là gốc chung của ….”
Lời giải
Đáp án đúng là: C
Vì mỗi điểm nằm trên đường thẳng là gốc của hai tia đối nhau nên điểm I bất kỳ nằm trên đường thẳng xy là gốc chung của hai tia đối nhau.
Lời giải
Đáp án đúng là: C
Vì điểm B nằm trên tia AM nên điểm B nằm giữa hai điểm A và M hoặc điểm M nằm giữa hai điểm A và B.
• Trường hợp 1: Điểm B nằm giữa hai điểm A và M
• Trường hợp 2: Điểm M nằm giữa hai điểm A và B
Lời giải
Đáp án đúng là: B
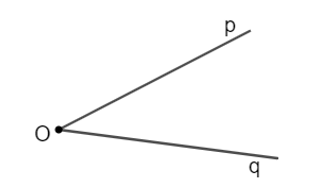
• Hai tia Op và Oq chung gốc nhưng không là hai tia đối nhau
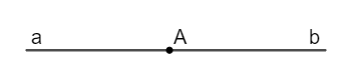
• Hai tia Aa và Ab là hai tia đối nhau có một điểm chung là điểm A.
• Hai tia Cb và Ab có nhiều điểm chung (B, Q) nhưng không nằm “chồng khít” lên nhau.
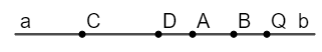
• Hai tia Cb và Db không chung gốc nhưng có nhiều điểm chung (A, B, Q).
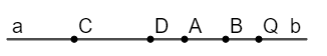
Câu 9
Cho đường thẳng ab. Lấy điểm I nằm trên đường thẳng ab, trên tia Ia lấy điểm M, trên tia Ib lấy điểm N. Một cặp tia đối nhau gốc I là
Cho đường thẳng ab. Lấy điểm I nằm trên đường thẳng ab, trên tia Ia lấy điểm M, trên tia Ib lấy điểm N. Một cặp tia đối nhau gốc I là
Lời giải
Đáp án đúng là: D
• Hai tia MI và NI là hai tia không chung gốc.
• Hai tia bI và aI là hai tia không chung gốc.
• Hai tia Ia và IM có chung gốc I nhưng không tạo thành một đường thẳng nên hai tia Ia và IM không là hai tia đối nhau.
• Hai tia IM và Ib có chung gốc là điểm I và tạo thành một đường thẳng nên hai tia IM và Ib là hai tia đối nhau.
Câu 10
Cho 4 điểm A, B, C, D (mỗi bộ 3 điểm không thẳng hàng). Vẽ được bao nhiêu tia mà mỗi tia đều chứa hai trong số các điểm đó?
Cho 4 điểm A, B, C, D (mỗi bộ 3 điểm không thẳng hàng). Vẽ được bao nhiêu tia mà mỗi tia đều chứa hai trong số các điểm đó?
Lời giải
Đáp án đúng là: C
• Chọn điểm A làm gốc, ta vẽ được 3 tia: AB, AC, AD.
• Chọn điểm B làm gốc, ta vẽ được 3 tia: BA, BC, BD.
• Chọn điểm C làm gốc, ta vẽ được 3 tia: CA, CB, CD.
• Chọn điểm D làm gốc, ta vẽ được 3 tia: DA, DB, DC.
Do đó, từ 4 điểm A, B, C, D (mỗi bộ 3 điểm không thẳng hàng), ta vẽ được 12 tia mà mỗi tia đều chứa hai trong số các điểm đó.
4.6
72 Đánh giá
50%
40%
0%
0%
0%