Bộ 5 đề thi cuối kì 1 Toán 6 Kết nối tri thức cấu trúc mới có đáp án - Đề 3

Hướng dẫn giải

Hướng dẫn giải

2. Ta có \[40 = {2^3} \cdot 5\,;\,\,36 = {2^2} \cdot {3^2}\].

Suy ra \[BCNN\left( {40,36} \right) = {2^3} \cdot {3^2} \cdot 5 = 360.\]

Do đó \[BC\left( {40,\,36} \right) = B\left( {360} \right) = \left\{ {0\,;\,\,360\,;\,\,720\,;\,\,...} \right\}.\]

Mà \(x\) là số tự nhiên và \[0 < x < 380\] nên \[x = 360.\]

Vậy \[x = 360.\]

Hướng dẫn giải

1. Các mặt hàng có giá tiền nhỏ hơn \(50\,\,000\) đồng trong bảng giá đã cho là: Thanh long Phan Thiết \[\left( {19\,000\,{\rm{vnd/kg}}} \right){\rm{,}}\] đầu cá hồi \[\left( {39\,900\,{\rm{vnd/kg}}} \right){\rm{,}}\] lốc 4 hộp sữa chua uống Yomost \(170\,\,{\rm{ml}}\) các loại \[\left( {22\,500\,{\rm{vnd/kg}}} \right){\rm{,}}\] sữa đặc Ngôi Sao Phương Nam xanh dương \(1,284\,\,{\rm{kg}}\) \[\left( {45\,500\,{\rm{vnd/kg}}} \right).\]

Do đó, tập hợp các mặt hàng có giá tiền nhỏ hơn \(50\,\,000\,{\rm{vnd}}\) đồng trong bảng giá là:

\(M = {\rm{\{ }}\)Thanh long Phan Thiết; đầu cá hồi; lốc 4 hộp sữa chua uống Yomost \(170\,\,{\rm{ml}}\) các loại; sữa đặc Ngôi Sao Phương Nam xanh dương \(1,284\,\,{\rm{kg\} }}.\)

2. Lợi nhuận của công ty An Bình sau 12 tháng kinh doanh là:

\[\left( {--70} \right) \cdot 4 + 60 \cdot 8 = 200\] (triệu đồng)

Vậy sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là 200 triệu đồng.

3. Gọi số học sinh của trường THCS đó là \(a\) (học sinh) \(\left( {a \in \mathbb{N},100 \le a < 250} \right)\).

Do khi xếp hàng 10 em thì thừa 8 em nên \(a\) chia 10 dư 8, hay \(\left( {a + 2} \right) \vdots 10\).

Khi xếp hàng 12 em thì thừa 10 em nên \(a\) chia 12 dư 10, hay \(\left( {a + 2} \right) \vdots 12\).

Khi xếp hàng 15 em thì thừa 13 em nên \(a\) chia 15 dư 13, hay \(\left( {a + 2} \right) \vdots 15\).

Từ đó suy ra \(a + 2 \in BC\left( {10,12,15} \right)\).

Ta có: \(10 = 2.5\); \(12 = {2^2}.3\); \(15 = 3.5\).

Do đó \(BCNN\left( {10,12,15} \right) = {2^2}.3.5 = 60\).

Khi đó \[a + 2 \in BC\left( {10,12,15} \right) = B\left( {60} \right) = \left\{ {0;60;120;180;240;300;360;...} \right\}\].

Mà \(100 \le a < 250\) nên \(102 \le a + 2 \le 252\), suy ra \(a + 2 \in \left\{ {120;180;240} \right\}\)

Do đó \(a \in \left\{ {118;178;238} \right\}\)

Mặt khác khi số học sinh của trường xếp hàng 17 thì vừa đủ nên \(a \vdots 17\)

Xét 3 trường hợp ở trên ta có \(a = 238\) thỏa mãn.

Vậy trường THCS đó có 238 học sinh.

Hướng dẫn giải

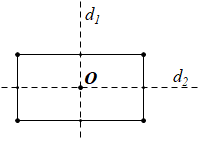
1. a) Tâm đối xứng \(O\) và các trục đối xứng \({d_1},{d_2}\) của hình chữ nhật đã cho được vẽ như hình dưới đây:

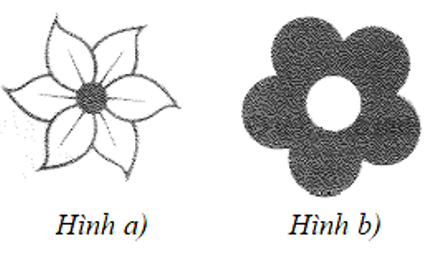
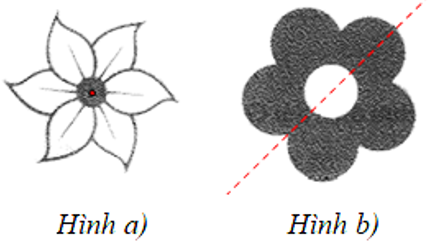
b) Bông hoa ở Hình a) có tâm đối xứng và bông hoa ở Hình b) có trục đối xứng:

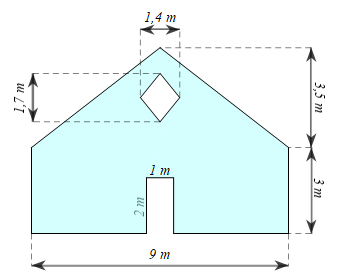
2. a) Diện tích cửa đi hình chữ nhật là: \(1.2 = 2\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Diện tích cửa thoáng hình thoi là: \(\frac{1}{2}.1,7.1,4 = 1,19\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Vậy diện tích cửa đi hình chữ nhật là \(2\,\,{{\rm{m}}^{\rm{2}}}\) và diện tích cửa thoáng hình thoi \(1,19\,\,{{\rm{m}}^{\rm{2}}}.\)

b) Diện tích của phần bức tường hình chữ nhật (không tính cửa đi) là:

\(9.3 - 2 = 25\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Diện tích của phần bức tường hình tam giác (không tính cửa thoáng hình thoi) là:

\(\frac{1}{2}.3,5.9 - 1,19 = 14,56\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Phần diện tích của bức tường cần sơn là:

\(25 + 14,56 = 39,56\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Số tiền bác Nam phải trả để sơn bức tường là:

\(39,56.30\,\,000 = 1\,\,186\,\,800\) (đồng).

Vậy bác Nam phải mất \(1\,\,186\,\,800\) đồng để sơn được bức tường đó.