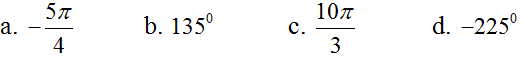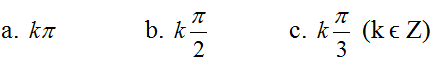Bài 1: Cung và góc lượng giác
27 người thi tuần này 4.6 11.7 K lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
a) Đổi 35o47’25’’ sang radian
b) Đổi 3 rad ra độ
Lời giải
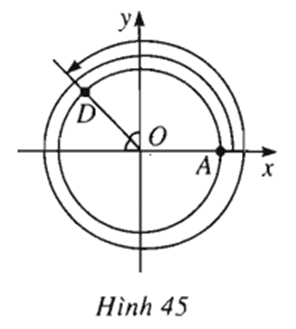
Cung lượng giác AD có số đo là
2π + π/2 + π/4 = 11π/4
Lời giải
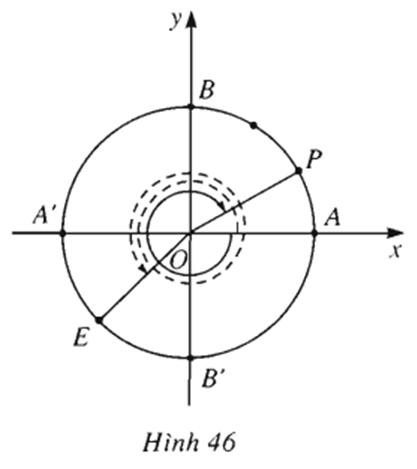
(OA, OE) = sđ cung(AE)= sđ cung(AB') + sđ cung(B'E) = - 90o + (-45)o = -135o = -3/4π (rad)
(OA, OP) = sđ cung(AP)= 1/3 sđ cung(AB) = 1/3 . 90° = 30o = π/6 rad.
Lời giải
Khi số đo hai cung lệch nhau k.2π (k ∈ Z) thì điểm cuối của chúng có thể trùng nhau.
Chẳng hạn các cung α = π/3 và β = π/3 + 2π , γ = π/3 - 2π có điểm cuối trùng nhau khi biểu diễn trên đường tròn lượng giác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.