10 Bài tập Hai tam giác đồng dạng và tính chất của hai tam giác đồng dạng (có lời giải)
37 người thi tuần này 4.6 486 lượt thi 10 câu hỏi 45 phút
🔥 Đề thi HOT:
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
20 câu trắc nghiệm Toán 8 Kết nối tri thức Ôn tập chương I (Đúng sai - trả lời ngắn) có đáp án
2 câu Trắc nghiệm Toán 8 Bài 10: Đường thẳng song song với một đường thẳng cho trước có đáp án (Vận dụng cao)
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
15 câu Trắc nghiệm Toán 8: Ôn tập chương 2 có đáp án (Thông hiểu)
11 câu Trắc nghiệm Toán 8 Bài 3: Rút gọn phân thức có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. ΔNMQ ᔕ ΔCAB;
B. ΔQMN ᔕ ΔCAB;
C. ΔQNM ᔕ ΔBAC;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
Vì ΔMNQ ᔕ ΔABC nên ta có các góc tương ứng bằng nhau là .
Khi viết tên tam giác đồng dạng các đỉnh phải ghi theo thứ tự các góc bằng nhau nên B đúng.
Câu 2
A. Hai tam giác bằng nhau thì đồng dạng với nhau;
B. Mỗi tam giác đồng dạng với chính nó;
C. Hai tam giác đồng dạng thì bằng nhau;
Lời giải
Đáp án đúng là: C
Đáp án A: Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng k = 1 nên A đúng.
Đáp án B: Mỗi tam giác đồng dạng với chính nó nên B đúng.
Đáp án C: Hai tam giác đồng dạng chưa chắc đã bằng nhau nên C sai.
Đáp án D: Hai tam giác gọi là đồng dạng với nhau nếu chúng có các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ nên D đúng.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
ΔMNQ đồng dạng với ΔOHK khi có các cặp góc bằng nhau và các cặp cạnh tương ứng tỉ lệ nên A đúng.
Câu 4
A. ;
B. 3;
C. 2;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
ΔABC ᔕ ΔDEF với tỉ số đồng dạng là .
Suy ra hay .
Vậy ΔDEF ᔕ ΔABC với tỉ số đồng dạng k = ![]() .
.
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
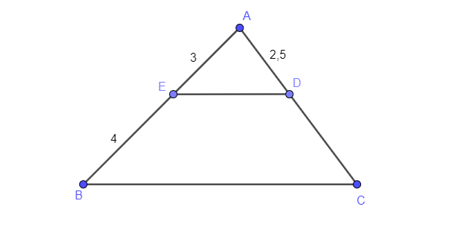
Vì DE là đường trung bình của tam giác ABC nên ta có:
+ (D là trung điểm AC).
+ (E là trung điểm AB).
+ và DE // BC (tính chất đường trung bình).
DE // BC suy ra (các góc đồng vị).
Suy ra ΔAED ᔕ ΔABC với tỉ số k = ![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
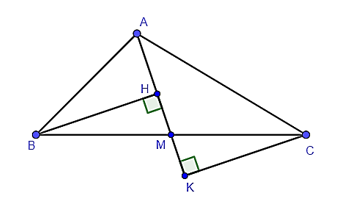
Câu 7
A. Tam giác AHB;
B. Tam giác HMC;
C. Tam giác AKC;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 12 cm;
B. 4 cm;
C. 36 cm;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. ΔMNQ ᔕ ΔABC với tỉ số đồng dạng k = 6;
B. ΔABC ᔕ ΔMNQ với tỉ số đồng dạng k =;
C. ΔABC ᔕ ΔMNQ với tỉ số đồng dạng k = 6;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. 3;
B. ;
C. 2;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.