10 Bài tập Tính độ dài đoạn thẳng và tỉ số của hai đoạn thẳng bằng cách sử dụng tính chất của đường phân giác (có lời giải)

Đáp án đúng là: B

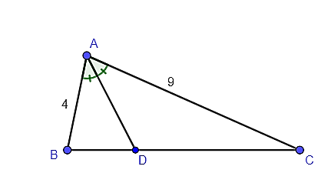
Tam giác ABC có AD là đường phân giác góc A.

Do đó ta có:

$\frac{\text{AC}}{\text{AB}}=\frac{\text{CD}}{\text{BD}}$ hay $\frac{\text{9}}{4}=\frac{\text{CD}}{\text{BD}}$  .

Đáp án đúng là: C

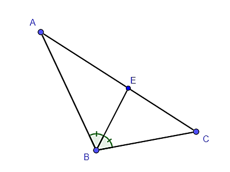
Tam giác ABC có BE là đường phân giác góc E.

Do đó ta có: $\frac{\text{AB}}{\text{BC}}=\frac{\text{AE}}{\text{EC}}$   hay $\frac{6}{\text{x}}=\frac{\text{5}}{\text{3}}$

Suy ra $\text{x}=\frac{6\cdot 3}{5}=3,6$  .

Đáp án đúng là: A

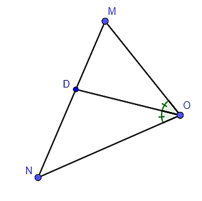
Tam giác OMN có OD là đường phân giác góc O.

Do đó ta có:  $\frac{\text{ON}}{\text{OM}}=\frac{\text{DN}}{\text{MD}}$.

Suy ra $\frac{\text{ON}}{\text{DN}}=\frac{\text{OM}}{\text{MD}}$  (tính chất của tỉ lệ thức).

Khi đó, $\frac{\text{OM}}{\text{MD}}=\frac{9}{7}$ .

Đáp án đúng là: D

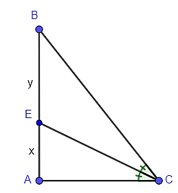
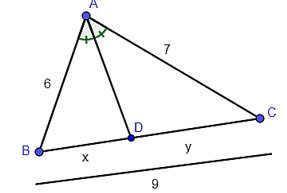
Tam giác ABC có CE là đường phân giác góc C.

Do đó ta có:  $\frac{\text{AC}}{\text{CB}}=\frac{\text{AE}}{\text{EB}}$hay  $\frac{\text{x}}{\text{y}}=\frac{6}{10}=\frac{3}{5}$ .

Suy ra $\text{x}=\frac{3}{5}\text{y}$ .

Vì AE + EB = AB hay x + y = 8

Do đó $\frac{3}{5}\text{y + y}=8$  , suy ra $\frac{8}{5}\text{y}=8$ .

Vậy y = 5 và x = 8 – 5 = 3.

Đáp án đúng là: A

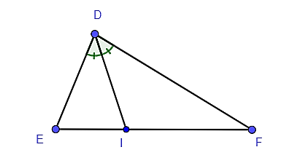
Tam giác DEF có DI là đường phân giác của góc D.

Do đó ta có: $\frac{\text{DE}}{\text{DF}}=\frac{\text{EI}}{\text{IF}}$  hay $\frac{\text{EI}}{\text{IF}}=\frac{5}{8}$  .

Tỉ số diện tích của tam giác DEI và DFI chính là tỉ số $\frac{\text{EI}}{\text{IF}}$   (vì hai tam giác này có chung đường cao hạ từ D đến EF).

Vậy tỉ số diện tích của tam giác DEI và tam giác DFI là $\frac{5}{8}$  .

Đáp án đúng là: C

Ta có MP = 2MN, suy ra $\frac{MN}{MP}=\frac{1}{2}$ .

Tam giác MNP có MO là đường phân giác góc M.

Do đó ta có: $\frac{\text{NO}}{\text{OP}}=\frac{\text{MN}}{\text{MP}}$  hay $\frac{\text{NO}}{\text{OP}}=\frac{1}{2}$  . Vậy (I) đúng.

Suy ra $\frac{\text{OP}}{\text{NO}}=2$ . Vậy (IV) sai.

Vì NO + OP = NP nên NO + 2NO = NP hay 3NO = NP

Suy ra  $\frac{\text{NO}}{\text{NP}}=\frac{1}{3}$ và $\frac{\text{OP}}{\text{NP}}=\frac{2}{3}$ . Vậy (II) sai, (III) đúng.

Vậy có 2 khẳng định đúng.

Đáp án đúng là: D

Vì I là giao điểm của ba đường phân giác trong tam giác ABC.

Do đó I cách đều ba cạnh của tam giác ABC (tính chất ba đường phân giác trong tam giác).

Suy ra IG = IH = IK.

Mà IG = 12 cm nên IK = 12 cm.

Đáp án đúng là: B

Tam giác ABC có AD là đường phân giác của góc A.

Do đó ta có $\frac{\text{AB}}{\text{AC}}=\frac{\text{BD}}{\text{DC}}$  hay $\frac{6}{7}=\frac{\text{x}}{\text{y}}$

Suy ra $\text{x}=\frac{6}{7}\text{y}$ .

Ta có BD + DC = BC hay x + y = 9.

Từ đó ta có $\frac{6}{7}\text{y}+\text{y}=9$ , suy ra $\frac{13}{7}\text{y}=9$  .

Vậy $\text{y}=\frac{63}{13}$  và  $\text{x}=\frac{54}{13}$.

Do đó $\text{y}-\text{x}=\frac{63}{13}-\frac{54}{13}=\frac{9}{13}$ .

Đáp án đúng là: C

Tam giác ABC có:

+ BI là đường phân giác của góc B.

Do đó ta có: $\frac{\text{AI}}{\text{IC}}=\frac{\text{AB}}{\text{BC}}$  hay $\frac{\text{AI}}{\text{IC}}=\frac{\text{m}}{\text{n}}$  (1).

+ CH là đường phân giác của góc C.

Do đó ta có: $\frac{\text{AH}}{\text{HB}}=\frac{\text{AC}}{\text{BC}}$  hay $\frac{\text{AH}}{\text{HB}}=\frac{\text{m}}{\text{n}}$ (2).

Từ (1) và (2) suy ra $\frac{\text{AH}}{\text{HB}}=\frac{\text{AI}}{\text{IC}}=\frac{\text{m}}{\text{n}}$ .

Theo định lí Thalès đảo ta suy ra HI // BC.

Theo (2) ta có $\frac{\text{AH}}{\text{HB}}=\frac{\text{m}}{\text{n}}$  nên $\frac{\text{AH+HB}}{\text{HB}}=\frac{\text{m + n}}{\text{n}}$   hay $\frac{\text{AB}}{\text{HB}}=\frac{\text{m + n}}{\text{n}}$  .

Suy ra  $\frac{\text{HB}}{\text{AB}}=\frac{\text{n}}{\text{m + n}}$, khi đó, $\frac{\text{HA}}{\text{AB}}=\frac{AB-HB}{AB}=1-\frac{HB}{AB}=\frac{\text{m}}{\text{m + n}}$  .

Vì HI // BC nên ta có: $\frac{\text{AH}}{\text{AB}}=\frac{\text{HI}}{\text{BC}}$ .

Suy ra $\text{HI}=\frac{\text{AH}}{\text{AB}}\cdot \text{BC=}\frac{\text{m}}{\text{m + n}}\cdot \text{n}=\frac{\text{mn}}{\text{m + n}}$ .

Đáp án đúng là: B

Tam giác ABC có:

+ BD là đường phân giác của góc B.

Do đó $\frac{\text{AD}}{\text{DC}}=\frac{\text{AB}}{\text{BC}}$   hay $\frac{\text{AB}}{\text{BC}}=\frac{1}{2}$ .

Suy ra BC = 2AB (1).

+ CE là đường phân giác của góc C.

Do đó $\frac{\text{AE}}{\text{EB}}=\frac{\text{AC}}{\text{BC}}$  hay $\frac{\text{AC}}{\text{BC}}=\frac{3}{4}$

Suy ra $\text{AC}=\frac{3}{4}\text{BC}$  (2).

Từ (1) và (2) suy ra $\text{AC}=\frac{3}{2}\text{AB}$  .

Chu vi tam giác ABC bằng:

AB + AC + BC = AB + $\frac{3}{2}\text{AB}$  + 2AB = $\frac{9}{2}\text{AB}$  = 18.

Suy ra AB = 4 (cm)

Vậy BC = 2 ⋅ 4 = 8 (cm), $\text{AC}=\frac{3}{2}\cdot \text{4 = 6}$  (cm).