Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án ( Đề 10)
19 người thi tuần này 4.6 1.9 K lượt thi 5 câu hỏi 50 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
Dạng 1. Vận dụng tính chất của hình bình hành để chứng minh các tính chất hình học có đáp án
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
10 câu Trắc nghiệm Toán 8 Bài 3: Tính chất đường phân giác của tam giác có đáp án (Thông hiểu)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
a) Chiều cao trung bình của trẻ 13 tuổi là: \[0,75 + 0,05 \cdot \left( {13 - 1} \right) = 1,35 \left( m \right).\]
b) Gọi \[y\] là chiều cao trung bình; \[x\] là độ tuổi của trẻ em.
Công thức mô tả sự phụ thuộc giữa chiều cao trung bình và độ tuổi của trẻ em Việt Nam là:
\[y = 0,75 + 0,25\left( {x - 1} \right).\]
Lời giải
a) ⦁ Vẽ đồ thị hàm số \(y = x + 3:\)
Cho \(x = 0,\) ta có \(y = 3;\)
Cho \(y = 0,\) ta có \(x = - 3.\)
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(\left( {0;3} \right)\) và \(\left( { - 3;0} \right).\)
⦁ Vẽ đồ thị hàm số \(y = - \frac{1}{2}x + 3:\)
Cho \(x = 0,\) ta có \(y = 3;\)
Cho \(y = 0,\) ta có \(x = 6.\)
Đồ thị hàm số \(y = - \frac{1}{2}x + 3\) là đường thẳng đi qua hai điểm \(\left( {0;3} \right)\) và \(\left( {6;0} \right).\)
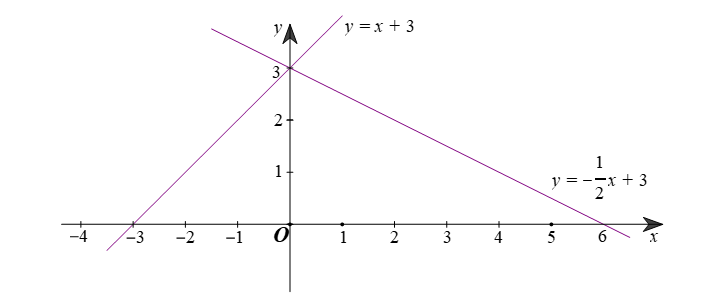
b)
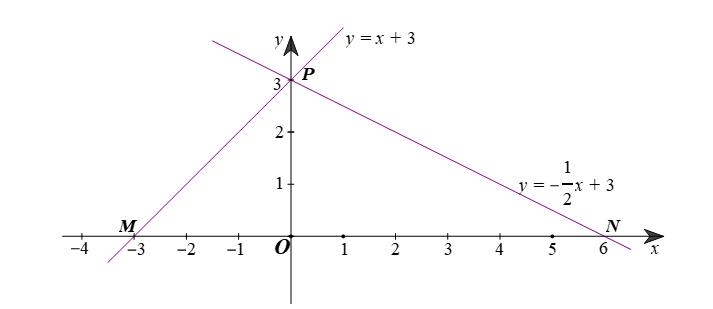
Giao điểm đồ thị của hàm số (1) với trục hoành là \(M\left( { - 3;0} \right);\)
Giao điểm đồ thị của hàm số (2) với trục hoành là \(N\left( {6;0} \right);\)
Giao điểm của hai đồ thị hàm số (1) và hàm số (2) là \(P\left( {0;3} \right).\)
Vậy \(M\left( { - 3;0} \right);\,\,N\left( {6;0} \right);\,\,P\left( {0;3} \right).\)
c) Tính độ dài các cạnh của \(\Delta MNP:\)
\(MN = MO + ON = 3 + 6 = 9{\rm{\;}}\left( {{\rm{cm}}} \right);\)
\(MP = \sqrt {M{O^2} + P{O^2}} = \sqrt {{3^2} + {3^2}} = \sqrt {18} = 3\sqrt 2 {\rm{\;}}\left( {{\rm{cm}}} \right);\)
\(NP = \sqrt {O{P^2} + O{N^2}} = \sqrt {{3^2} + {6^2}} = \sqrt {45} = 3\sqrt 5 {\rm{\;}}\left( {{\rm{cm}}} \right).\)
Diện tích của \(\Delta MNP\) là: \({S_{\Delta MNP}} = \frac{1}{2}PO \cdot MN = \frac{1}{2} \cdot 3 \cdot 9 = \frac{{27}}{2}\,\,\left( {\;{\rm{c}}{{\rm{m}}^2}} \right).\)
Chu vi tam giác \(MNP\) là: \(9 + 3\sqrt 2 + 3\sqrt 5 {\rm{\;}}\left( {{\rm{cm}}} \right).\)
Lời giải
a) Vì công ty lựa chọn khấu hao từng chiếc xe theo phương pháp khấu hao đường thẳng trong vòng 8 năm. Điều này có nghĩa là sau mỗi năm, mỗi chiếc xe sẽ giảm giá \[640:8 = 80\] (triệu đồng) nên ta có sau \[x\] năm thì mỗi chiếc xe giảm \[80x\] (triệu đồng).
Hàm số bậc nhất biểu thị giá trị sổ sách \[V\] (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi \[x\] (năm) của nó là: \[V = 640--80x = --80x + 640\] (triệu đồng).
Hàm số \[V = --80x + 640\] đi qua các điểm \[\left( {0;{\rm{ }}640} \right)\] và \[\left( {8;{\rm{ }}0} \right).\]
Đồ thị hàm số như hình dưới đây.
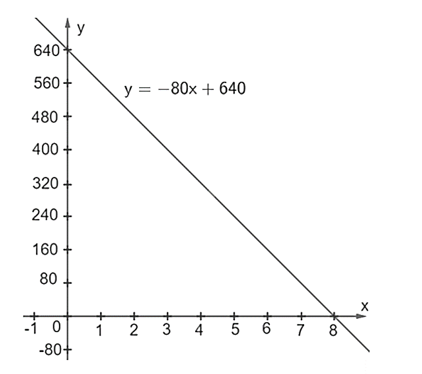
Chú ý: Vì số lớn nên ta chia khoảng cách giữa 2 trục Ox và Oy là khác nhau
b) Để giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng thì: \(V = 160\)
Hay:
\[--80x + 640 = 160\]
\[--80x = --480\]
\(x = 6\)
Vậy sau 6 năm thì giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng.
Lời giải
Hướng dẫn giải
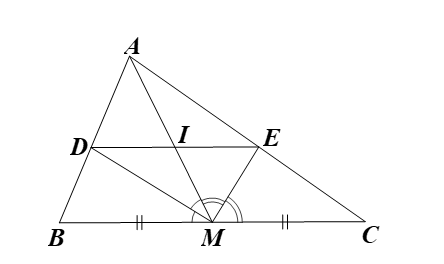
a) Xét \(\Delta ABM\) có \(MD\) là đường phân giác của \(\widehat {AMB}\) nên \(\frac{{MA}}{{MB}} = \frac{{DA}}{{DB}}\) \(\left( 1 \right)\) (tính chất đường phân giác của tam giác).
Xét \[\Delta ACM\] có \(ME\) là đường phân giác của \(\widehat {AMC}\) nên \(\frac{{MA}}{{MC}} = \frac{{EA}}{{EC}}\) \(\left( 2 \right)\) (tính chất đường phân giác của tam giác).
Do \(AM\) là đường trung tuyến của \[\Delta ABC\] nên \(M\) là trung điểm của \(BC,\) hay \(MB = MC = \frac{1}{2}BC.\,\,\,\left( 3 \right)\)
Từ \(\left( 1 \right),\,\,\left( 2 \right)\) và \(\left( 3 \right)\) ta có \(\frac{{DA}}{{DB}} = \frac{{EA}}{{EC}}.\)
Theo tính chất tỉ lệ thức ta có \(\frac{{DA}}{{DA + DB}} = \frac{{EA}}{{EA + EC}},\) hay \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}},\) suy ra \(AD \cdot AC = AE \cdot AB.\)
Xét \[\Delta ABC\] có \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}},\) theo định lí Thalès đảo ta có \[DE\,{\rm{//}}\,BC.\]
b) Xét \(\Delta ABM\) có \(DI\,{\rm{//}}\,BM,\) theo hệ quả định lí Thalès ta có \(\frac{{DI}}{{BM}} = \frac{{AI}}{{AM}}.\)
Xét \[\Delta ACM\] có \(IE\,{\rm{//}}\,MC,\) theo hệ quả định lí Thalès ta có \[\frac{{IE}}{{MC}} = \frac{{AI}}{{AM}}.\]
Do đó \(\frac{{DI}}{{BM}} = \frac{{IE}}{{MC}}.\)
Mà \(MB = MC\) (chứng minh ở câu a) nên \(DI = IE,\) hay \[I\] là trung điểm của \(DE.\)
c) Ta có \(MB = MC = \frac{1}{2}BC = \frac{1}{2} \cdot 30 = 15{\rm{\;cm}}.\)
Theo câu a, ta có \(\frac{{DA}}{{DB}} = \frac{{MA}}{{MB}},\) suy ra \[\frac{{DA}}{{DA + DB}} = \frac{{MA}}{{MA + MB}} = \frac{{10}}{{10 + 15}} = \frac{{10}}{{25}} = \frac{2}{5}.\]
Do đó \(\frac{{AD}}{{AB}} = \frac{2}{5}.\)
Xét \(\Delta ABC\) có \(DE\,{\rm{//}}\,BC,\) theo hệ quả định lí Thalès ta có \(\frac{{DE}}{{BC}} = \frac{{AD}}{{AB}} = \frac{2}{5}.\)
Suy ra \(DE = \frac{2}{5}BC = \frac{2}{5} \cdot 30 = 12{\rm{\;}}\left( {{\rm{cm}}} \right).\)
Lời giải
Ta có \(AB \bot AE;\,\,CD \bot AE\) nên \(CD\,{\rm{//}}\,AB\).
Xét tam giác \(ABE\) có \(CD\,{\rm{//}}\,AB\), ta có
\[\,\frac{{DE}}{{AB}} = \frac{{EC}}{{EA}}\] (hệ quả của định lí Thalès).
Hay \[\frac{{1,5}}{{AB}} = \frac{2}{{2 + 8}}\] suy ra \[AB = 7,5\,\,{\rm{m}}\].
Vậy chiều cao của cây là \[7,5\,\,{\rm{m}}\].