Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 3)
41 người thi tuần này 4.3 11.4 K lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 5 đề thi giữa kì 1 Toán 6 Cánh diều (2022-2023) có đáp án - Đề 05
Bộ 5 đề thi giữa kì 1 Toán 6 Cánh diều (2022-2023) có đáp án - Đề 04
Bộ 5 đề thi giữa kì 1 Toán 6 Cánh diều (2022-2023) có đáp án - Đề 03
Bộ 5 đề thi giữa kì 1 Toán 6 Cánh diều (2022-2023) có đáp án - Đề 02
Bộ 5 đề thi giữa kì 1 Toán 6 Cánh diều (2022-2023) có đáp án - Đề 01
Bộ 5 đề thi giữa kì 1 Toán 6 Kết nối tri thức (2022-2023) có đáp án - Đề 05
Bộ 5 đề thi giữa kì 1 Toán 6 Kết nối tri thức (2022-2023) có đáp án - Đề 04
Bộ 5 đề thi giữa kì 1 Toán 6 Kết nối tri thức (2022-2023) có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải:
a) (15,25 + 3,75).4 + (20,71 + 5,29).5
= 19.4 + 26.5
= 76 + 130
= 206
b) \[\frac{4}{{20}} + \frac{{16}}{{42}} + \frac{6}{{15}} + \frac{{ - 3}}{5} + \frac{2}{{21}} + \frac{{ - 10}}{{21}} + \frac{3}{{20}}\]
\[ = \frac{1}{5} + \frac{8}{{21}} + \frac{2}{5} + \frac{{ - 3}}{5} + \frac{2}{{21}} + \frac{{ - 10}}{{21}} + \frac{3}{{20}}\]
\[ = \frac{1}{5} + \frac{2}{5} + \frac{{ - 3}}{5} + \frac{8}{{21}} + \frac{2}{{21}} + \frac{{ - 10}}{{21}} + \frac{3}{{20}}\]
\[ = \left( {\frac{1}{5} + \frac{2}{5} + \frac{{ - 3}}{5}} \right) + \left( {\frac{8}{{21}} + \frac{2}{{21}} + \frac{{ - 10}}{{21}}} \right) + \frac{3}{{20}}\]
\[ = \frac{{1 + 2 + \left( { - 3} \right)}}{5} + \frac{{8 + 2 + \left( { - 10} \right)}}{{21}} + \frac{3}{{20}}\]
\( = \frac{0}{5} + \frac{0}{{21}} + \frac{3}{{20}}\)
\( = 0 + 0 + \frac{3}{{20}}\)
\[ = \frac{3}{{20}}\]
c) \[\frac{5}{{11}}.\frac{5}{7} + \frac{5}{{11}}.\frac{2}{7} + \frac{6}{{11}}\]
\[ = \left( {\frac{5}{{11}}.\frac{5}{7} + \frac{5}{{11}}.\frac{2}{7}} \right) + \frac{6}{{11}}\]
\[ = \frac{5}{{11}}.\left( {\frac{5}{7} + \frac{2}{7}} \right) + \frac{6}{{11}}\]
\( = \frac{5}{{11}}.\frac{7}{7} + \frac{6}{{11}}\)
\( = \frac{5}{{11}}.1 + \frac{6}{{11}}\)
\[ = \frac{5}{{11}} + \frac{6}{{11}}\]
\( = \frac{{5 + 6}}{{11}}\)
\( = \frac{{11}}{{11}}\)
= 1.
d) \(\left( { - \frac{5}{{24}} + 0,75 + \frac{7}{{12}}} \right):\left( { - 2\frac{1}{8}} \right)\)
\( = \left( { - \frac{5}{{24}} + \frac{3}{4} + \frac{7}{{12}}} \right):\left( { - \frac{{17}}{8}} \right)\)
\( = \left( { - \frac{5}{{24}} + \frac{{18}}{{24}} + \frac{{14}}{{24}}} \right):\left( { - \frac{{17}}{8}} \right)\)
\( = \frac{{ - 5 + 18 + 14}}{{24}}:\left( { - \frac{{17}}{8}} \right)\)
\( = \frac{9}{8}.\left( { - \frac{8}{{17}}} \right)\)
\[ = \frac{{9.\left( { - 8} \right)}}{{8.17}}\]
\[ = - \frac{9}{{17}}\]
Lời giải
Hướng dẫn giải:
a) \(\frac{2}{3}\,\, + \,\,\frac{1}{3} \cdot \,\,x\, = \,\frac{5}{6}\)
\({\mkern 1mu} {\mkern 1mu} \frac{1}{3}{\mkern 1mu} \cdot \,x{\mkern 1mu} \, = \,\,\frac{5}{6} - \frac{2}{3}{\mkern 1mu} \)
\({\mkern 1mu} \frac{1}{3}{\mkern 1mu} \, \cdot \,x{\mkern 1mu} \, = {\mkern 1mu} {\mkern 1mu} \frac{5}{6}{\mkern 1mu} \, - \,{\mkern 1mu} \frac{4}{6}\)
\({\mkern 1mu} \frac{1}{3} \cdot \,{\mkern 1mu} x{\mkern 1mu} \, = {\mkern 1mu} \,{\mkern 1mu} \frac{1}{6}{\mkern 1mu} \)
\(x{\mkern 1mu} {\mkern 1mu} = \,{\mkern 1mu} {\mkern 1mu} \frac{1}{6}\,{\mkern 1mu} {\mkern 1mu} :{\mkern 1mu} {\mkern 1mu} \,{\mkern 1mu} \frac{1}{3}\)
\(x{\mkern 1mu} \, = \,{\mkern 1mu} {\mkern 1mu} \frac{1}{6}\,{\mkern 1mu} \cdot \,\frac{3}{1}\)
\(x{\mkern 1mu} \, = \,{\mkern 1mu} \frac{1}{2}\).
Vậy \(x{\mkern 1mu} \, = \,{\mkern 1mu} \frac{1}{2}\).
b) 53,2 : (x – 3,5) + 45,8 = 99
53,2 : (x – 3,5) = 99 – 45,8
53,2 : (x – 3,5) = 53,2
x – 3,5 = 53,2 : 53,2
x – 3,5 = 1
x = 1 + 3,5
x = 4,5.
Vậy x = 4,5.
c) \[\left( {4\frac{1}{2} - 2x} \right).1\frac{4}{{61}} = 6\frac{1}{2}\].
\[\left( {\frac{9}{2} - 2x} \right).\frac{{65}}{{61}} = \frac{{13}}{2}\]
\[\frac{9}{2} - 2x = \frac{{13}}{2}:\frac{{65}}{{61}}\]
\[\frac{9}{2} - 2x = \frac{{13}}{2}.\frac{{61}}{{65}}\]
\[\frac{9}{2} - 2x = \frac{{13}}{2}.\frac{{61}}{{5.13}}\]
\[\frac{9}{2} - 2x = \frac{{61}}{{10}}\]
\[2x = \frac{9}{2} - \frac{{61}}{{10}}\]
\[2x = \frac{{45}}{{10}} - \frac{{61}}{{10}}\]
\[2x = \frac{{ - 16}}{{10}}\]
\[2x = \frac{{ - 8}}{5}\]
\[x = \frac{{ - 8}}{5}:2\]
\[x = \frac{{ - 8}}{5}.\frac{1}{2}\]
\[x = \frac{{ - 4}}{5}\]
Vậy \[x = \frac{{ - 4}}{5}\].
d) \(\frac{1}{2}\,\, \cdot \,x\,\, + \,\,150\% \cdot \,\,x\,\, = \,\,\,2022\)
\(\frac{1}{2}{\mkern 1mu} {\mkern 1mu} \cdot \,x{\mkern 1mu} \,{\mkern 1mu} + \,{\mkern 1mu} {\mkern 1mu} \frac{{150}}{{100}}\,\, \cdot \,{\mkern 1mu} x\,{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 2022\)
\(\frac{1}{2}{\mkern 1mu} {\mkern 1mu} \cdot \,{\mkern 1mu} x{\mkern 1mu} {\mkern 1mu} \, + \,{\mkern 1mu} {\mkern 1mu} \frac{3}{2}{\mkern 1mu} \, \cdot {\mkern 1mu} {\mkern 1mu} \,x{\mkern 1mu} \,{\mkern 1mu} = \,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 2022\)
\(x.\left( {\frac{1}{2} + \frac{3}{2}} \right) = 2022\)
\(x\,.{\mkern 1mu} \,\frac{4}{2}{\mkern 1mu} \, = {\mkern 1mu} \,2022\)
x . 2 = 2022
x = 2022 : 2
x = 1011
Vậy x = 1011.
Lời giải
Hướng dẫn giải
Diện tích trồng cây ăn trái của mảnh vườn là: \[\frac{2}{3}.870 = 580\](m2).
Diện tích trồng rau của mảnh vườn là: 25% . 870 = 217,5 (m2).
Diện tích trồng hoa của mảnh vườn là: 870 – (580 + 217,5) = 72,5 (m2).
Vậy diện tích trồng hoa của mảnh vườn là 72,5 m2.
Lời giải
Hướng dẫn giải
a) Quan sát biểu đồ tranh ta thấy có bốn hình ü bạn An đi xe máy cùng bố mẹ.
Mà mỗi ü ứng với 3 buổi học.
Số buổi học An đến trường bằng xe máy cùng bố mẹ là: 4.3 = 12 (buổi học).
b) Số buổi học bạn An đi xe bus đến trường là: 3.3 = 9 (buổi học).
Số buổi học bạn An đi phương tiện khác đến trường là: 2.3 = 6 (buổi học).
Ta có bảng thống kê sau:
|
Phương tiện |
Xe bus |
Xe máy (bố mẹ chở) |
Phương tiện khác |
|
Số lượng học sinh |
9 |
12 |
6 |
c) Tổng số buổi học bạn An đi các phương tiện đến trường trong tháng 3 là:
9 + 12 + 6 = 27 (buổi học)
Xác suất bạn An đến trường bằng xe bus là: \(\frac{9}{{27}}.100\% = 33,33333..\) %
Làm tròn đến chữ số thập phân thứ nhất ta được kết quả là 33,3%.
Lời giải
Hướng dẫn giải
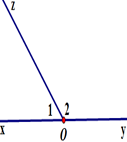
|
Tên góc (cách viết thông thường) |
Kí hiệu |
Tên đỉnh |
Tên cạnh |
|
Góc \(xOz\), góc \[{\rm{zOx}}\], góc \({O_1}\) |
\(\widehat {xOz},\widehat {zOx},\widehat {{O_1}}\) |
O |
Ox, Oz |
|
Góc \(yOz\), góc \[{\rm{zOy}}\], góc \({O_2}\) |
\(\widehat {yOz},\widehat {zOy},\widehat {{O_2}}\) |
O |
Oy, Oz |
|
Góc \(xOy\), góc \[{\rm{yOx}}\], góc \(O\) |
\(\widehat {xOy},\widehat {yOx},\widehat O\) |
O |
Ox, Oy |
b)

Vì điểm M là trung điểm của IC nên ta có: \(IM = \frac{{IC}}{2}\)
Điểm \(N\)là trung điểm của ID nên: \(IN = \frac{{ID}}{2}\)
Mặt khác: I nằm giữa C và D nên ta có IC + ID = CD.
Do đó: \(MN = IM + IN = \frac{{IC + ID}}{2} = \frac{{CD}}{2} = \frac{8}{2} = 4\) cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.