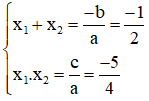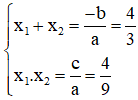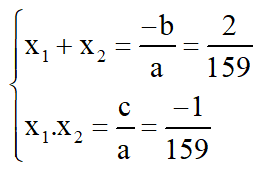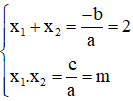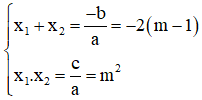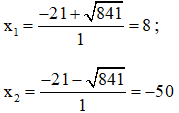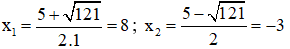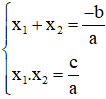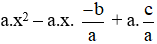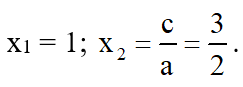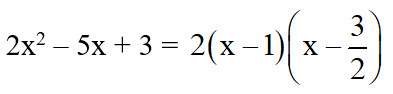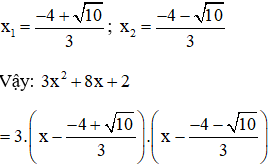Giải bài tập SGK Toán 9 tập 2 hay nhất Luyện tập trang 54
20 người thi tuần này 4.6 1.8 K lượt thi 5 câu hỏi
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
12 bài tập Một số bài toán thực tế liên quan đến độ dài cung tròn, diện tích hình quạt tròn và hình vành khuyên có lời giải
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
15 câu trắc nghiệm Toán 9 Kết nối tri thức Bài 13. Mở đầu về đường tròn có đáp án
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
a) Phương trình
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm
Theo hệ thức Vi-et ta có:
b) Phương trình .
Có a = 9; b' = -6; c = 4
⇒ Phương trình có nghiệm kép
Theo hệ thức Vi-et ta có:
c) Phương trình
Có a = 5; b = 1; c = 2
⇒ Phương trình vô nghiệm.
d) Phương trình
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt
Theo hệ thức Vi-et ta có:
Lời giải
a) Phương trình
Có a = 1; b = -2; c = m nên b’= -1
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et:
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
b) Phương trình
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ m ≤ 1/2.
Khi đó, theo định lý Vi-et:
Vậy với m ≤ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng
Lời giải
a)
Có a = 1,5; b = -1,6; c = 0,1
⇒ a + b + c = 1,5 – 1,6 + 0,1 = 0
⇒ Phương trình có hai nghiệm
d)
Có a = m – 1 ; b = - (2m + 3) ; c = m + 4
⇒ a + b + c = (m – 1) – (2m + 3) + m + 4 = m -1 – 2m – 3 + m + 4 = 0
⇒ Phương trình có hai nghiệm
Lời giải
a) S = 42; P = 441
⇒ u và v là hai nghiệm của phương trình:
Có:
⇒ Phương trình có nghiệm kép
Vậy u = v = 21.
b) S = -42; P = -400
⇒ u và v là hai nghiệm của phương trình:
Có
⇒ Phương trình có hai nghiệm phân biệt:
Vậy u = 8; v = -50 hoặc u = -50; v = 8.
c) u – v = 5 ⇒ u + (-v) = 5
u.v = 24 ⇒ u.(-v) = -uv = -24.
Ta tìm u và –v. Từ đó, ta dễ dàng tính được u và v.
S= u + (-v) = 5; P = u. (-v) = -24 ⇒
⇒ u và –v là hai nghiệm của phương trình:
Có
⇒ Phương trình có hai nghiệm phân biệt
⇒ u = 8; -v = -3 hoặc u = -3; -v = 8
⇒ u = 8; v = 3 hoặc u = -3; v = -8.
Lời giải
* Chứng minh:
Phương trình có hai nghiệm
⇒ Theo định lý Vi-et:
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
=
* Áp dụng:
a)
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm
Vậy:
b)
Có a = 3; b' = 4; c = 2
⇒
⇒ Phương trình có hai nghiệm phân biệt: