Bài tập chuyên đề Toán 7 Dạng 4: Hai tam giác bằng nhau. Các trường hợp bằng nhau của hai tam giác có đáp án
69 người thi tuần này 4.6 1.8 K lượt thi 52 câu hỏi 60 phút
🔥 Đề thi HOT:
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 4
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
* Tìm cách giải. Khi viết hai tam giác bằng nhau thì các đỉnh tương ứng phải viết theo cùng một thứ tự. Viết như vậy, thì việc suy ra các cặp cạnh tương ứng bằng nhau mới chính xác.
* Trình bày lời giải.
a) ; ; .
Lời giải
b) suy ra ; ; .
Chu vị bằng: .
Chu vi bằng: .
Lời giải
* Tìm cách giải. Bài toán yêu cầu tính số đo góc của tam giác nên từ , chúng ta chỉ quan tâm tới cặp góc tương ứng bằng nhau.
* Trình bày lời giải.
(cặp góc tương ứng).
Vì ; mà , nên
;
.
có ; .
Vì nên .
Câu 4
Cho góc nhọn xOy. Lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy sao cho OA=OB. Vẽ hai cung tròn tâm A và tâm B có cùng bán kính nhỏ hơn OA sao cho chúng cắt nhau tại 2 điểm C và D. Chứng minh rằng:
a,
Lời giải
Giải
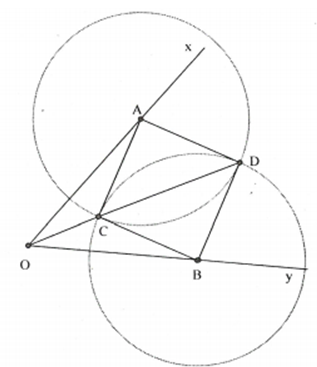
a) Xét và có: OA=OB (giả thiết), (bán kính bằng nhau), OC cạnh chung.
.
Lời giải
b) nên
tương tự: nên .
Nên C, D cùng thuộc tia phân giác góc xOy hay O, C, D thẳng hàng.
Câu 6
Cho có . Lấy M thuộc cạnh AB; lấy N thuộc tia đối của tia CA sao cho CM=BM. Gọi I là một điểm sao cho ; IM=IN. Chứng minh rằng: .
Cho có . Lấy M thuộc cạnh AB; lấy N thuộc tia đối của tia CA sao cho CM=BM. Gọi I là một điểm sao cho ; IM=IN. Chứng minh rằng: .
Lời giải
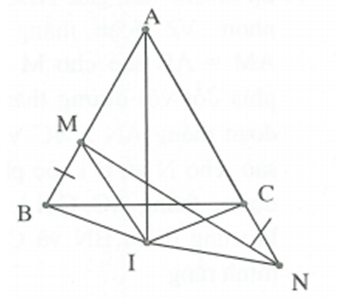
Ta có .
.
Suy ra , mà đó là hai góc kề bù nên , hay .
* Nhận xét.
Đây là bài toán khó. Để chứng minh chúng ta suy nghĩ và chứng minh là điều cần thiết. Sau đó, chúng ta hãy tìm các cặp tam giác bằng nhau mà trong các tam giác ấy có chứa hoặc .
Câu 7
Cho tam giác ABC có . Kẻ tia phân giác góc cắt AC tại D. Trên cạnh BC lấy điểm M sao cho BM=BA.
a) Chứng minh rằng .
Cho tam giác ABC có . Kẻ tia phân giác góc cắt AC tại D. Trên cạnh BC lấy điểm M sao cho BM=BA.
a) Chứng minh rằng .
Lời giải
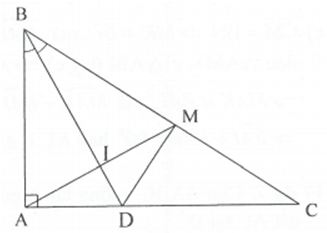
a) và có ; ; BD là cạnh chung .
.Lời giải
Xét và có AB=MB; ; BI là cạnh chung
mà nên , suy ra: .
Lời giải
c) nên ;
vuông nên .
Suy ra do đó .
Câu 10
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng ; AM=AB sao cho M và C khác phía đối với đường thẳng AB. Vẽ đoạn thẳng và AN=AC sao cho N và B khác phía đối với đường thẳng AC. Gọi I, K lần lượt là trung điểm BN và CM. Chứng minh rằng:
a,
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng ; AM=AB sao cho M và C khác phía đối với đường thẳng AB. Vẽ đoạn thẳng và AN=AC sao cho N và B khác phía đối với đường thẳng AC. Gọi I, K lần lượt là trung điểm BN và CM. Chứng minh rằng:
a,
Lời giải
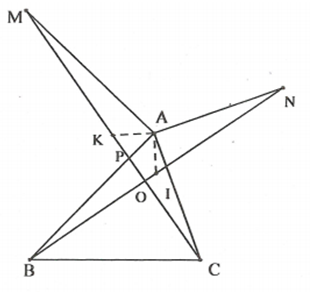
a, nên
Lời giải
b) . Và .
Gọi P là giao điềm của AB và CM
Ta có: (vì vuông)
.
Lời giải
c) , mà ;
nên .
; mà
hay .
Lời giải
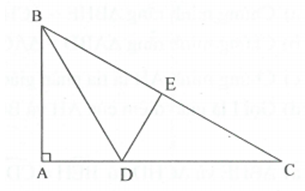
a) Gọi E là trung điểm của BC. Suy ra
và có BA=BE ; (giả thiết); BD là cạnh chung
.
Xét và có: ; BE=CE ; DE chung
Lời giải
b)
Mặt khác: (Vì vuông tại A)
.
Câu 15
Cho tam giác ABC có . Các tia phân giác góc B, góc C cắt nhau tại O và cắt AC; AB theo thứ tự D; E. Chứng minh rằng: OD=OE.
Cho tam giác ABC có . Các tia phân giác góc B, góc C cắt nhau tại O và cắt AC; AB theo thứ tự D; E. Chứng minh rằng: OD=OE.
Lời giải
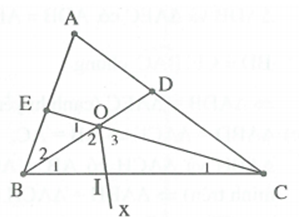
có
Mà nên .
Ta có .
có
Nên .
- Kẻ Ox là tia phân giác góc , cắt BC tại I nên .
Xét và có (giả thiết); ; BO là cạnh chung
do đó . Suy ra .
- Chứng minh tương tự ta có nên OD= OI.
Vậy .
* Nhận xét.
- Để chứng minh OE=OD, ta chưa thể ghép chúng vào hai tam giác nào bằng nhau được. Do vậy, ta nghĩ đến cách kẻ đường phụ. Cho số đo góc A ta liên hệ với bài đã biết nên tính được số đo góc BOC và góc BOE nên dựng được điểm I.
- Bài toán còn có cách khác, là lấy điểm I trên BC sao cho BI=BE, sau đó chứng minh rồi chứng minh .
- Từ cách trên ta còn suy ra kết quả đẹp là .
Câu 16
Cho tam giác ABC. Từ B kẻ ; . Gọi H là giao điểm của BD và CE. Biết rằng .
a) Chứng minh rằng
Cho tam giác ABC. Từ B kẻ ; . Gọi H là giao điểm của BD và CE. Biết rằng .
Lời giải
a)
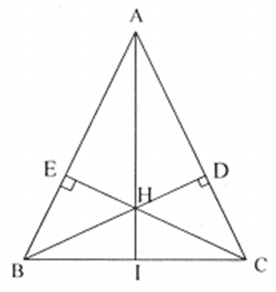
và có ; HD=HE;
.
Lời giải
b, mà HD=HE
và có ; BD=CE; chung
(cạnh huyền – góc nhọn).
Lời giải
c) .
và có ; AH là cạnh chung; (chứng minh trên)
là tia phân giác của .
Lời giải
d) và có ; ; AI là cạnh chung
; mà hay .
Lời giải
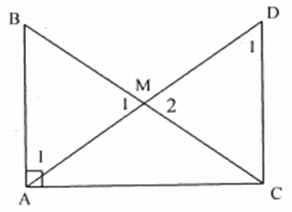
* Tìm cách giải. Để chứng minh ta cần chứng minh . Về mặt suy luận, ta cần dựng một đoạn thẳng bằng rồi chứng minh đoạn thẳng đó bằng BC.
* Trình bày lời giải.
Trên tia đối của tia MA lấy điểm D sao cho . Suy ra
và có ; ; nên .
Suy ra ; nên .
và có ; , AC chung suy ra
hay .
* Nhận xét. Bài này là một tính chất thú vị của tam giác vuông, thường được sử dụng trong những bài nối trung điểm của cạnh huyền với đỉnh góc vuông.
Lời giải
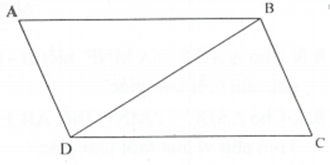
(cặp so le trong)
(cặp so le trong)
và có , BD là cạnh chung, .
Suy ra .
Lời giải
Hướng dẫn: suy ra: ; mà
Ta có: nên
có
;
Vậy ; ; .
Lời giải
Hướng dẫn: ; BC= NP; AC= MP (cặp cạnh tương ứng).
Vì , mà nên
Do đó chu vi là: .
Vì nên chu vi bằng chu vi và bằng 14cm.
Lời giải
Hướng dẫn: ; ; (cặp cạnh tương ứng).
Vì .
Áp dụng tính chất dãy tỉ số bằng nhau:
; .
Vậy: ; ; .
Lời giải
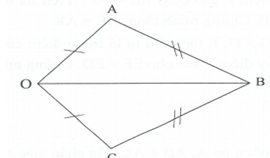
Hướng dẫn: và có ; ; OB chung
Lời giải
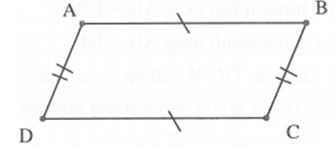
AB=CD; AD=BC; AC cạnh chung
Nên
Suy ra .
Mà hai góc ở vị trí so le trong .
mà hai góc ở vị trí so le trong .Lời giải
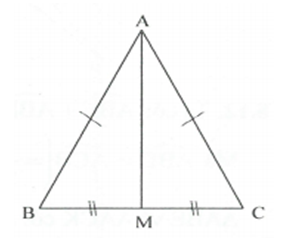
Hướng dẫn: và có AM chung; AB=AC ; BM=CM
(góc tương ứng)
.
(góc tương ứng).
Mà nên .
cóCâu 28
Cho vuông tại A. Tia phân giác của cắt AC ở D; E là một điểm trên cạnh BC sao cho BE=BA.
a) Chứng minh rằng: .
Cho vuông tại A. Tia phân giác của cắt AC ở D; E là một điểm trên cạnh BC sao cho BE=BA.
a) Chứng minh rằng: .
Lời giải
Hướng dẫn:
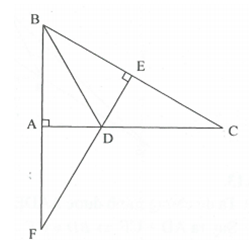
a) và có ; ; BD chung
.
Lời giải
b,
Lời giải
c,
và
Câu 31
Cho tam giác ABC nhọn. Kẻ , . Trên tia đối của tia BD lấy điểm H sao cho . Trên tia đối của tia CE lấy điểm K sao cho . Chứng minh:
a,
Cho tam giác ABC nhọn. Kẻ , . Trên tia đối của tia BD lấy điểm H sao cho . Trên tia đối của tia CE lấy điểm K sao cho . Chứng minh:
a,
Lời giải
Hướng dẫn:
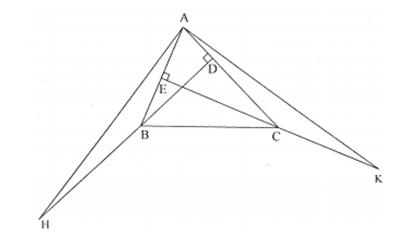
a) có
có
Từ (1) và (2), suy ra: do đó .
Lời giải
b) và có ; ;
.Câu 33
Cho tam giác ABC có . Tia phân giác góc B cắt AC ở D. Trên tia đối BD lấy điểm E sao cho BE= AC . Trên tia đối CB lấy điểm K sao cho CK= AB. Chứng minh rằng: .
Cho tam giác ABC có . Tia phân giác góc B cắt AC ở D. Trên tia đối BD lấy điểm E sao cho BE= AC . Trên tia đối CB lấy điểm K sao cho CK= AB. Chứng minh rằng: .
Lời giải
Hướng dẫn:
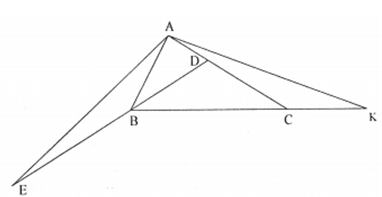
Ta có: ; (cặp góc kề bù)
Mà .
và có: AB=CK ; ; BE=AC
Câu 34
Cho . Gọi D; E theo thứ tự là trung điểm của AB, AC. Trên tia đối của tia ED lấy điểm F sao cho EF=ED. Chứng minh:
a, ,
Cho . Gọi D; E theo thứ tự là trung điểm của AB, AC. Trên tia đối của tia ED lấy điểm F sao cho EF=ED. Chứng minh:
a, ,
Lời giải
Hướng dẫn:
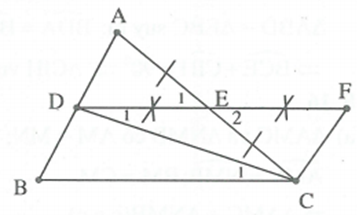
a) Ta dễ chứng minh được
Suy ra
Và , mà hai góc ở vị trí so le trong nên .
Lời giải
b) Xét và có BD=FC (chứng minh trên); (so le trong ); CD là cạnh chung
do đó: .Lời giải
c) (chứng minh trên) nên , mà hai góc ở vị trí so le trong suy ra .
* Nhận xét. Từ kết luận , chúng ta còn suy ra được:Câu 37
Cho vuông tại A, . Tia phân giác của cắt AC tại D. Trên cạnh BC lấy điểm E sao cho . Vẽ AH vuông góc với BC tại H.
a) Chứng minh rằng .
Cho vuông tại A, . Tia phân giác của cắt AC tại D. Trên cạnh BC lấy điểm E sao cho . Vẽ AH vuông góc với BC tại H.
a) Chứng minh rằng .
Lời giải
a) và có
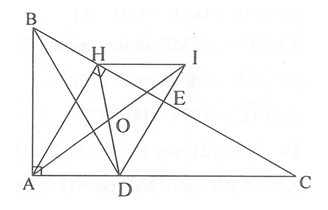
(giả thiết); ; BD là cạnh chung
.
Lời giải
b)
,
Mà .Câu 39
c) Trên tia DE lấy điểm I sao cho DI= AH. Gọi O là trung điểm của đoạn thẳng DH. Chứng minh rằng ba điểm A, O, I thẳng hàng
Lời giải
c) (cặp góc so le trong).
và có ; ; AH=ID
Mà (kề bù) .
Suy ra A, O, I thẳng hàng.Câu 40
Cho có . Trên nửa mặt phẳng bờ BC chứa điểm A. Vẽ tia Bx vuông góc với BC. Trên tia Bx lấy điểm D sao cho DB=BC. Trên nửa mặt phẳng bờ AB chứa điểm C vẽ tia By vuông góc với BA. Trên tia By lấy điểm E sao cho . Chứng minh rằng:
a,
Cho có . Trên nửa mặt phẳng bờ BC chứa điểm A. Vẽ tia Bx vuông góc với BC. Trên tia Bx lấy điểm D sao cho DB=BC. Trên nửa mặt phẳng bờ AB chứa điểm C vẽ tia By vuông góc với BA. Trên tia By lấy điểm E sao cho . Chứng minh rằng:
a,
Lời giải
a)
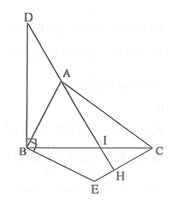
Xét và có ;
(cùng phụ với góc ABC);
.
Lời giải
b) Gọi H, I là giao điểm của đường thẳng AD với CE và BC. suy ra: mà
vuông, hay .Câu 42
Cho có . Gọi M là trung điểm cạnh BC. Trên nửa mặt phẳng bờ AB không chứa điểm C kẻ tia Ax vuông góc với AB, trên tia Ax lấy điểm D sao cho AD= AB. Trên nửa mặt phẳng bờ AC không chứa điểm B kẻ Ay vuông góc với AC. Trên tia Ay lấy điểm E sao cho . Trên tia đối tia MA lấy MN= MA. Chứng minh rằng:
a,
Cho có . Gọi M là trung điểm cạnh BC. Trên nửa mặt phẳng bờ AB không chứa điểm C kẻ tia Ax vuông góc với AB, trên tia Ax lấy điểm D sao cho AD= AB. Trên nửa mặt phẳng bờ AC không chứa điểm B kẻ Ay vuông góc với AC. Trên tia Ay lấy điểm E sao cho . Trên tia đối tia MA lấy MN= MA. Chứng minh rằng:
a,
Lời giải
a)
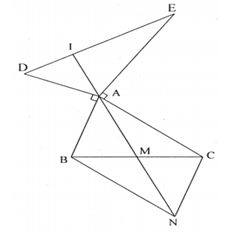
và có AM= MN; ; BM= CM
mà
Lời giải
b) Ta có ;
(chứng minh trên)
Xét và có AD= BA; ; AE= BN
; mà .
Lời giải
c) Gọi I là giao điểm của đường thẳng AM và DE.
(chứng minh trên)
Mà
Từ (1) và (2) suy ra: hay .Câu 45
Để đo khoảng cách AB mà không đo trực tiếp, người ta đã thực hiện như sau:
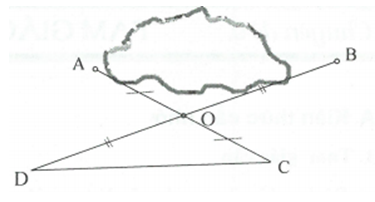
- Chọn vị trí điểm O.
- Lấy điểm C trên tia đối tia OA sao cho .
- Lấy điểm D trên tia đối tia OB sao cho .
- Đo độ dài đoạn thẳng CD, đó chính là khoảng cách AB. Hãy giải thích tại sao?
Để đo khoảng cách AB mà không đo trực tiếp, người ta đã thực hiện như sau:

- Chọn vị trí điểm O.
- Lấy điểm C trên tia đối tia OA sao cho .
- Lấy điểm D trên tia đối tia OB sao cho .
- Đo độ dài đoạn thẳng CD, đó chính là khoảng cách AB. Hãy giải thích tại sao?
Lời giải
Hướng dẫn: .
Câu 46
Cho tam giác ABC có . Các tia phân giác của BE; CF của và cắt nhau tại I (E, F lần lượt thuộc cạnh AC, AB). Trên cạnh BC lấy hai điểm M, N sao cho .
a) Tính số đo của .
Lời giải
a)
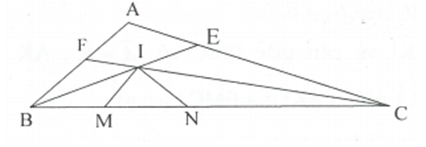
có .
Ta có: .
có :Lời giải
b) .
và có ; CI là cạnh chung;
Chứng minh tương tự ta có:
Từ (1) và (2), ta có: .Câu 48
Cho tam giác ABC có , tia phân giác của cắt BC tại D. Trên AD lấy điểm O, trên tia đối của tia AC lấy điểm M sao cho . Trên tia đối của tia AB lấy điểm N sao cho . Chứng minh rằng .
Cho tam giác ABC có , tia phân giác của cắt BC tại D. Trên AD lấy điểm O, trên tia đối của tia AC lấy điểm M sao cho . Trên tia đối của tia AB lấy điểm N sao cho . Chứng minh rằng .
Lời giải
Hướng dẫn:
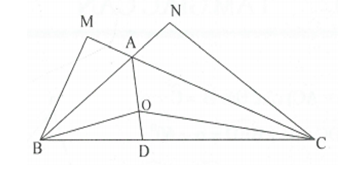
có .
Ta có AD là tia phân giác .
và có ; AB chung;
Chứng minh tương tự, ta có:
Từ (1) và (2), suy ra: .Lời giải
a)
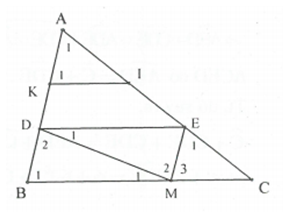
Kẻ
Tam giác DEM và tam giác MBD có ; DM chung;
nên suy ra BD=ME ; DE= BM .
Ta có nên ;
Lại có nên .
- Tam giac AKI và tam giác EMC có ;Lời giải
Câu 51
Cho vuông tại A có AB= AC . Lấy M thuộc . Kẻ BD và CE vuông góc với đường thẳng AM. Chứng minh rằng:
a) .
Cho vuông tại A có AB= AC . Lấy M thuộc . Kẻ BD và CE vuông góc với đường thẳng AM. Chứng minh rằng:
a) .
Lời giải
a)
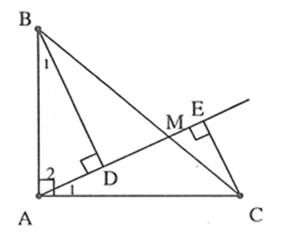
Xét và có ; AB= AC (giả thiết); (cùng phụ với )
do đó (cạnh huyền – góc nhọnLời giải
b) nên ; AD= CE do đó . Vậy .
* Nhận xét. Để chứng minh một đoạn thẳng bằng tổng hay một hiệu hai đoạn thẳng ta thường biến đổi đoạn thẳng đó thành hai đoạn cùng nằm trên một đường thẳng và sử dụng cộng, trừ đoạn thẳn368 Đánh giá
50%
40%
0%
0%
0%