Đề kiểm tra Toán 9 Chân trời sáng tạo Chương 4 có đáp án - Đề 1
40 người thi tuần này 4.6 60 lượt thi 11 câu hỏi 45 phút
🔥 Đề thi HOT:
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
37 K lượt thi
4 câu hỏi
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
4.3 K lượt thi
12 câu hỏi
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
36.8 K lượt thi
3 câu hỏi
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
10 K lượt thi
188 câu hỏi
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
10.6 K lượt thi
5 câu hỏi
Bộ 10 đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 1
6.1 K lượt thi
13 câu hỏi
Trắc nghiệm Bài tập lý thuyết Liên hệ giữa phép nhân, phép chia và phép khai phương có đáp án
4.7 K lượt thi
10 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. \[\cos \alpha = \frac{{MP}}{{NP}}.\]
B. \[\cos \alpha = \frac{{MN}}{{MP}}.\]
C. \[\cos \alpha = \frac{{MN}}{{NP}}.\]
D. \[\cos \alpha = \frac{{MP}}{{MN}}.\]
Lời giải
Chọn A
![Chọn A Theo định nghĩa tỉ số lượng giác trong tam giác vuông, ta có tam giác \[MNP\] vuông tại \[M\] nên \[\cos \alpha = \frac{{MP}}{{NP}}.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/41-1761181199.png)
Câu 2
![Chọn B Xét \[\Delta ABC\] vuông tại \[A\] có góc \[x\] và góc \[y\] là hai góc phụ nhau nên \[\sin y = \cos x \approx 0,78\] và \[\tan y = \cot x \approx 1,25\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/7-1761181536.png)
A. \[\sin {\rm{ }}y \approx 0,75\,;{\rm{ }}\tan y \approx \;1,45.\]
B. \[\sin {\rm{ }}y \approx 0,78\,;{\rm{ }}\tan y \approx \;1,25.\]
C. \[\sin {\rm{ }}y \approx 0,35\,;{\rm{ }}\tan y \approx \;1,35.\]
D. \[\sin {\rm{ }}y \approx 0,45\,;{\rm{ }}\tan y \approx \;1,15.\]
Lời giải
Chọn B
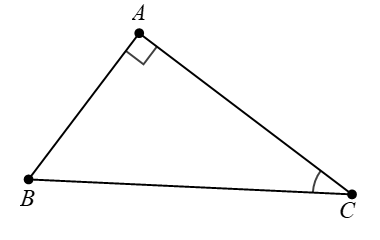
Xét \[\Delta ABC\] vuông tại \[A\] có góc \[x\] và góc \[y\] là hai góc phụ nhau nên
\[\sin y = \cos x \approx 0,78\] và \[\tan y = \cot x \approx 1,25\].
Câu 3
A. \(BC = 10\).
B. \(BC = 11\).
C. \(BC = 9\).
D. \(BC = 12\).
Lời giải
Chọn A
![Cho tam giác \[ABC\]có \(AB = 16\,;\,\,AB = 14\) và \(\widehat B = 60^\circ \). Độ dài cạnh \(BC\) là A. \(BC = 10\). B. \(BC = 11\). C. \(BC = 9\). D. \(BC = 12\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/14-1761181882.png)
Kẻ đường cao \(AH\).
Xét tam giác vuông \(ABH\), ta có: \(BH = AB.\cos B = AB.\cos 60^\circ = 16.\frac{1}{2} = 8\)
\(AH = AB.\sin B = AB.\sin 60^\circ = 16.\frac{{\sqrt 3 }}{2} = 8\sqrt 3 \).
Áp dụng định lý Pythagore vào tam giác \(AHC\) vuông \(H,\) ta có:
\(H{C^2} = A{C^2} - A{H^2} = {14^2} - {\left( {8\sqrt 3 } \right)^2} = 196 - 192 = 4\).
Suy ra \(HC = 2\).
Vậy \(BC = CH + HB = 2 + 8 = 10\).
Câu 4
A. \(15\;\,{\rm{m}}\).
B. \(16\;\,{\rm{m}}\).
C. \(18\;\,{\rm{m}}\).
D. \(12\;\,{\rm{m}}\).
Lời giải
Chọn B
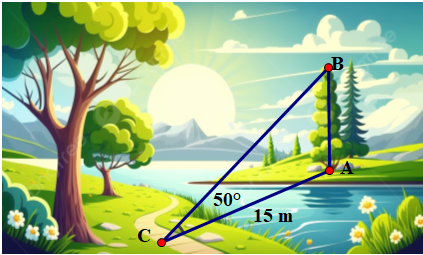
Xét \(\Delta ABC\) vuông tại \(A\), ta có:
\(\tan \widehat {ACB} = \frac{{AB}}{{AC}}\) hay \(\tan 50^\circ = \frac{{AB}}{{15}}\).
Suy ra \(AB = 15 \cdot \tan 50^\circ \approx 18\;\,({\rm{m)}}\).
Vậy chiều cao \[AB\] của cây khoảng 18 m.
Câu 5
A. \[AB = \frac{{5\sqrt 3 }}{3}\,\,{\rm{cm}}\,;\,\,BC = \frac{{20\sqrt 3 }}{3}\,\,{\rm{cm}}\].
B. \(AB = \frac{{10\sqrt 3 }}{3};\,\,BC = \frac{{14\sqrt 3 }}{3}\).
C. \[AB = \frac{{10\sqrt 3 }}{3}\,\,{\rm{cm}}\,;\,\,BC = 20\sqrt 3 \,\,{\rm{cm}}\].
D. \(AB = \frac{{10\sqrt 3 }}{3}\,\,{\rm{cm}};\,\,BC = \frac{{20\sqrt 3 }}{3}\,\,{\rm{cm}}\).
Lời giải
Chọn D
Xét tam giác \(ABC\) vuông tại \(A\) có:
• \(\tan C = \frac{{AB}}{{AC}}\) nên \(AB = AC \cdot \tan C = 10\tan 30^\circ = \frac{{10\sqrt 3 }}{3}\,\,{\rm{cm}}\);
• \(\cos C = \frac{{AC}}{{BC}}\) nên \(BC = \frac{{AC}}{{\cos C}} = \frac{{10}}{{\frac{{\sqrt 3 }}{2}}} = \frac{{20\sqrt 3 }}{3}\,\,{\rm{cm}}\).
Vậy \(AB = \frac{{10\sqrt 3 }}{3}\,\,{\rm{cm}};\,\,BC = \frac{{20\sqrt 3 }}{3}\,\,{\rm{cm}}\).
Câu 6
A. \[23,38\,\,{\rm{m}}\].
B. \[21,84\,\,{\rm{m}}\].
C. \[23,39\,\,{\rm{m}}\].
D. \[21,85\,\,{\rm{m}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Hỏi tòa nhà đó cao bao nhiêu tầng, biết rằng mỗi tầng cao \[2\,\,{\rm{m}}?\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/57-1761200288.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo