Giải SBT Toán 10 Bài 7. Các khái niệm mở đầu có đáp án
30 người thi tuần này 4.6 820 lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Lời giải
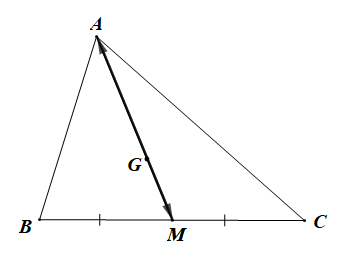
Ta có: M là trung điểm của BC và G là trọng tâm của tam giác ABC
Nên trung tuyến AM đi qua điểm G.
+ Hai vectơ \(\overrightarrow {GA} \) và \[\overrightarrow {GM} \] cùng phương vì chúng có giá trùng nhau.
Do đó khẳng định a) là đúng.
+ Hai vectơ \(\overrightarrow {GA} \) và \[\overrightarrow {GM} \] ngược hướng
Do đó khẳng định b) là sai và khẳng định c) là đúng.
+ Vì G là trọng tâm tam giác ABC nên \(AG = \frac{2}{3}AM\)
AM = 3MG.
Do đó \(\left| {\overrightarrow {AM} } \right| = 3\left| {\overrightarrow {MG} } \right|\)
Do đó khẳng định d) là đúng.
Vậy các khẳng định đúng là: a), c) và d).
Lời giải
Lời giải
Vì vectơ \(\overrightarrow 0 \) cùng phương với mọi vectơ nên:
+ Vectơ \(\overrightarrow 0 \) cùng phương với \(\overrightarrow a \)
+ Vectơ \(\overrightarrow 0 \) cùng phương với \(\overrightarrow b \)
Do đó có một vectơ \(\overrightarrow 0 \) cùng phương với cả \(\overrightarrow a \) và \(\overrightarrow b \).
Lời giải
Lời giải
Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) cùng phương và cùng khác vectơ \(\overrightarrow 0 \) nên chúng có thể cùng hướng hoặc ngược hướng nhau.
Trường hợp 1: Nếu \[\overrightarrow a \] cùng hướng với \(\overrightarrow b \) (hoặc \(\overrightarrow a \) cùng hướng với \(\overrightarrow c \))
Thì khi đó có hai vectơ cùng hướng.
Trường hợp 2: Nếu \[\overrightarrow a \] ngược hướng với cả \(\overrightarrow b \) và \(\overrightarrow c \)
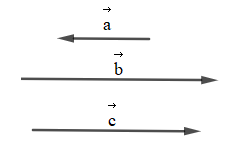
Vì \[\overrightarrow a \] ngược hướng với \(\overrightarrow b \), \[\overrightarrow a \] ngược hướng với \(\overrightarrow c \)
Nên khi đó \(\overrightarrow b \) và \(\overrightarrow c \) cùng hướng với nhau.
Do đó có hai vectơ trong ba vectơ cùng hướng với nhau
Vậy có ít nhất hai vectơ trong ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) có cùng hướng.
Lời giải
Lời giải
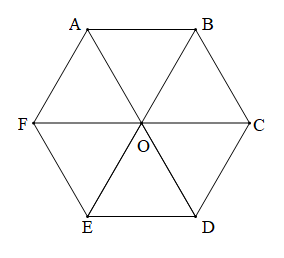
Do ABCDEF là lục giác đều tâm O nên:
+ Các cặp cạnh đối diện bằng nhau: AB = ED, BC = FE, CD = FA;
+ Ba đường chéo chính AD, BE, CF đồng quy tại trung điểm của mỗi đường;
+ Mỗi đường chéo chính song song với một cặp cạnh có đầu mút không thuộc đường chéo ấy.
a) Các vectơ khác vectơ - không và cùng phương với vectơ \(\overrightarrow {OA} \) mà có hai điểm mút lấy từ các điểm O, A, B, C, D, E, F là: \(\overrightarrow {OA} ,\overrightarrow {AO} ,\overrightarrow {OD} ,\overrightarrow {DO} ,\overrightarrow {BC} ,\overrightarrow {CB} ,\overrightarrow {EF} ,\overrightarrow {FE} ,\overrightarrow {DA} ,\overrightarrow {AD} .\)
b) Vectơ bằng vectơ \(\overrightarrow {AB} \) mà có hai điểm mút lấy từ các điểm O, A, B, C, D, E, F là: \(\overrightarrow {AB} ,\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} .\)
Lời giải
Lời giải
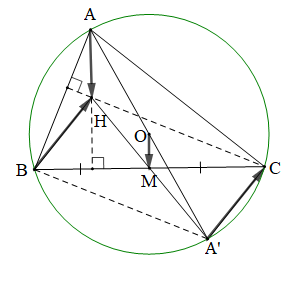
Vì H là trực tâm tam giác ABC nên CH ⊥ AB
Mặt khác AA' là đường kính của (O), B ∈ (O) nên \(\widehat {ABA'} = 90^\circ \)
Do đó AA' ⊥ AB
Suy ra CH // AA' (từ vuông góc đến song song)
Chứng minh tương tự ta cũng có BH // A'C
Tứ giác BHCA' có CH // AA' và BH // A'C
Suy ra BHCA' là hình bình hành
Do đó \(\overrightarrow {BH} = \overrightarrow {{\rm{A'C}}} .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.