Bài tập Tổng và hiệu của hai vecto có đáp án
38 người thi tuần này 4.6 1.5 K lượt thi 13 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
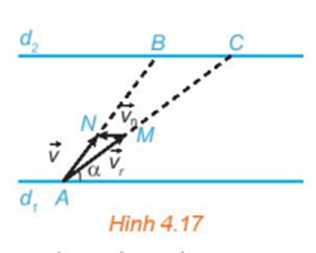
Sau bài học này ta sẽ giải quyết bài toán này như sau:
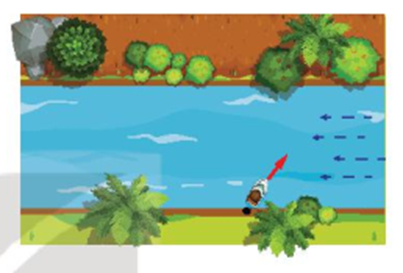
Ta biểu thị hai bờ sông là hai đường thẳng song song d1, d2 (H.4.17). Giả sử tàu xuất phát từ và bánh lái luôn được giữ để tàu tạo với bờ một góc . Gọi và lần lượt là vận tốc riêng của tàu và vận tốc dòng nước. Gọi M, N là các điểm sao cho
Khi đó tàu chuyển động với vectơvận tốc thực tế là
Gọi B, C tương ứng là giao điểm của AN, AM với d2. Tàu chuyển động thẳng từ A đến B với vận tốc thực tế là , do đó thời gian cần thiết để tàu sang được bờ d2 là . Mặt khác, không đổi nên nhỏ nhất ⇔ AC nhỏ nhất
Vậy để tàu sang được bờ bên kia nhanh nhất, ta giữ bánh lái để tàu luôn vuông góc với bờ.
Lời giải
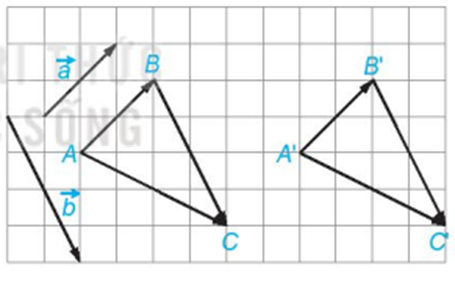
Ta có:
cùng hướng với và độ dài bằng độ dài .
Ta lại có:
cùng hướng với và độ dài bằng độ dài .
cùng hướng với và độ dài bằng độ dài .
ABB’A’ là hình bình hành (1)
Ta có:
cùng hướng với và độ dài bằng độ dài .
Ta lại có:
cùng hướng với và độ dài bằng độ dài .
cùng hướng với và độ dài bằng độ dài .
BB’C’C là hình bình hành (2)
Từ (1) và (2) suy ra AA’C’C là hình bình hành
Vậy .
Lời giải
Vì ABCD là hình bình hành nên ta có:
Vậy .
Lời giải
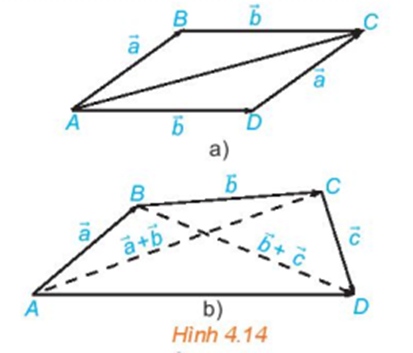
Trong Hình 4.14a:
Ta có:
Trong Hình 4.14b:
Ta có:
Lời giải
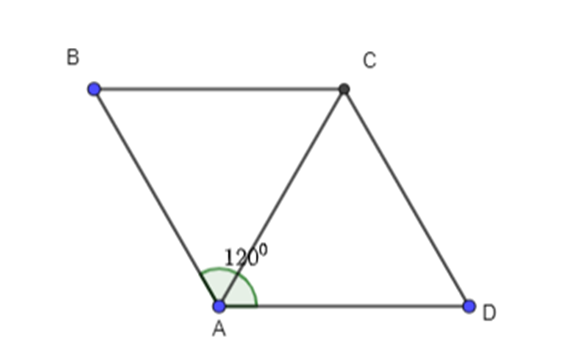
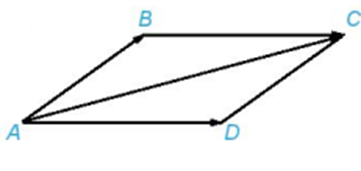
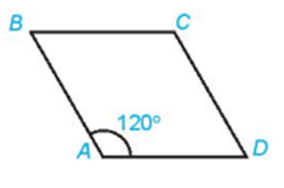
+ Tứ giác ABCD là hình thoi nên ABCD cũng là hình bình hành
Do đó (quy tắc hình bình hành)
Vì ABCD là hình thoi nên AB= BC và AC là tia phân giác ( tính chất hình thoi)
Xét ΔABC có AB = BC và
⇒ ΔABC đều
⇒ AC = AB = BC = 1
Suy ra
Ta có: (quy tắc ba điểm).
Vậy độ dài của các vectơ và đều bằng 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.