10 Bài tập Vận dụng tính chất ba đường cao, đường trung trực trong tam giác để giải quyết các bài toán khác (có lời giải)
53 người thi tuần này 4.6 378 lượt thi 10 câu hỏi 40 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 4
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
A. giao của ba đường trung tuyến của ∆ABC;
B. giao của ba đường phân giác của ∆ABC;
C. giao của ba đường trung trực của ∆ABC;
Lời giải
Hướng dẫn giải:
Đáp án đúng là:C

Gọi đường tròn đi qua ba điểm A, B, C có tâm O ta có OA = OB = OC.
Ba điểm phân biệt A, B, C không thẳng hàng tạo thành tam giác ABC.
Vì OA = OB = OC nên O là giao điểm ba đường trung trực của tam giác ABC.
Vậy đường tròn đi qua ba điểm A, B, C có tâm O là giao của ba đường trung trực của ∆ABC và bán kính bằng OA.
Câu 2
A. KA < KB = KC;
B. KA > KB = KC;
C. KA = KB < KC;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
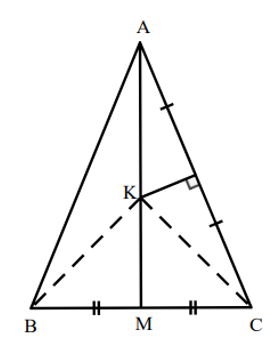
Vì ∆ABC cân tại A nên đường trung tuyến AM cũng là đường trung trực.
Mà K là giao điểm các đường trung trực của BC, AC.
Vì vậy KA = KB = KC.
Câu 3
A. Chỉ (I) đúng;
B. Chỉ (II) đúng;
C. Cả (I), (II) đều đúng;
D. Cả (I), (II) đều sai.
Lời giải
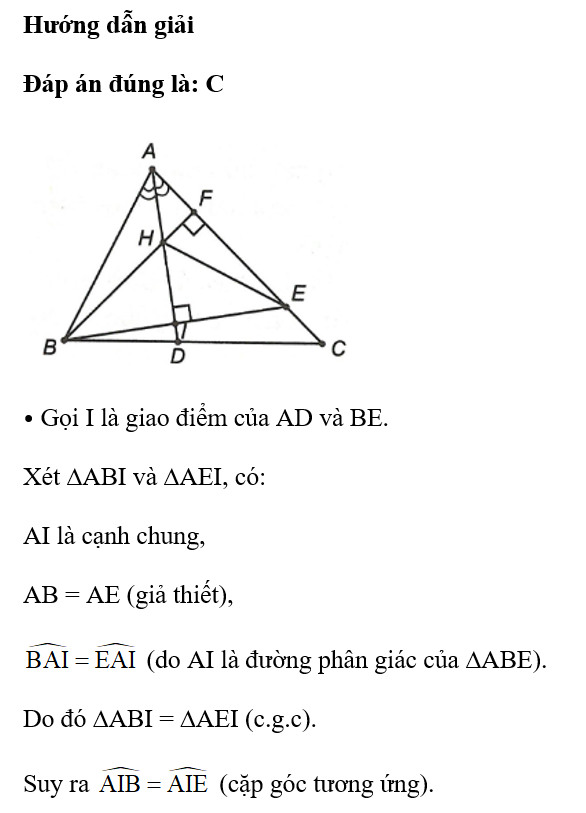

Câu 4
A. Giao của hai đường trung trực;
B. Giao của hai đường phân giác;
C. Giao của hai đường trung tuyến;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
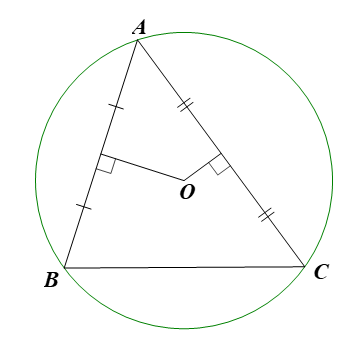
Ta thực hiện các bước:
Bước 1. Lấy ba điểm A, B, C trên đường viền ngoài của mảnh gỗ hình tròn.
Bước 2. Vẽ tam giác ABC.
Bước 3. Vẽ hai đường trung trực của tam giác đó, hai đường này cắt nhau tại một điểm. Đây chính là tâm của tấm gỗ hình tròn cần xác định.
Câu 5
A. OA là đường trung trực của BC;
B. ∆HBD = ∆KCE;
C. BD = DE = EC;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: C
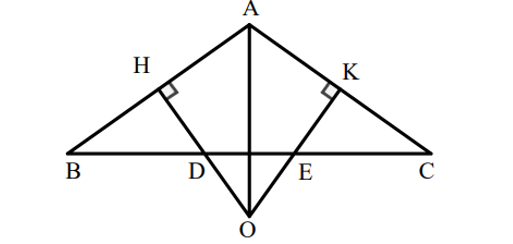
Gọi O là giao điểm các đường trung trực của AB và AC.
Suy ra O nằm trên đường trung trực của BC.
Mà ∆ABC cân tại A nên AB = AC nên A nằm trên đường trung trực của BC.
Do đó AO là đường trung trực của BC.
Gọi H là trung điểm của AB nên
Gọi K là trung điểm của AC nên
Mà AB = AC nên AH = BH = AK = CK.
Xét ∆BHD (vuông tại H) và ∆CKE (vuông tại K) có:
BH = CK và (do vì ∆ABC cân tại A)
Do đó ∆HBD = ∆KCE (cạnh góc vuông – góc nhọn kề)
Suy ra BD = CE (hai cạnh tương ứng) và (hai góc tương ứng)
Nên (đối đỉnh), suy ra ∆ODE cân tại O.
Vậy A, B, D là các khẳng định đúng. Ta chọn phương án C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.
B. CI ⊥ AB;
C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. giao điểm của hai đường trung trực của AB và AC;
B. giao điểm của hai đường phân giác góc A và góc B;
C. giao điểm của hai đường đường cao kẻ từ A và B;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 45°;
B. 50°;
C. 40°;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. Ba điểm D, A, E thẳng hàng;
B. DE ngắn nhất khi và chỉ khi AM ngắn nhất;
C. AM ngắn nhất khi và chỉ khi M là hình chiếu của A lên cạnh BC;
D. Cả A, B, C đều đúng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.