Bộ 5 đề thi cuối kì 1 Toán 6 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 4
12 người thi tuần này 4.6 93 lượt thi 6 câu hỏi 60 phút
🔥 Đề thi HOT:
Dạng 4: Một số bài tập nâng cao về lũy thừa
16.3 K lượt thi
10 câu hỏi
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
12.5 K lượt thi
31 câu hỏi
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
10.8 K lượt thi
40 câu hỏi
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
5 K lượt thi
10 câu hỏi
Dạng 1. Biểu diễn một tập hợp cho trước
5.4 K lượt thi
45 câu hỏi
Dạng 1: Thực hiện tính, viết dưới dạng lũy thừa
15.2 K lượt thi
45 câu hỏi
5 câu Trắc nghiệm Toán 6 Cánh diều Bài 1: Tập hợp có đáp án ( Nhận biết )
5.1 K lượt thi
5 câu hỏi
20 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án (Phần 2)
3.8 K lượt thi
19 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
|
a) \(4 \cdot {5^2} - 18:{3^2}\) \( = 4 \cdot 25 - 18:9\) \( = 100 - 2\) \( = 98\). c) \[25 \cdot 75 - 3 \cdot 70 + 25 \cdot 125 - 3 \cdot 130\] \[ = \left( {25 \cdot 75 + 25 \cdot 125} \right) - \left( {3 \cdot 70 + 3 \cdot 130} \right)\] \[ = 25 \cdot \left( {75 + 125} \right) - 3 \cdot \left( {70 + 130} \right)\] \[ = 25 \cdot 200 - 3 \cdot 200\] \[ = 200 \cdot \left( {25 - 3} \right)\] \[ = 200 \cdot 22\] \[ = 4\,\,400\]. |
b) \[\left( {1\,\,267 - 196} \right) - \left( {267 + 304} \right)\] \[ = 1\,\,267 - 196 - 267 - 304\] \[ = \left( {1\,\,267 - 267} \right) - \left( {196 + 304} \right)\] \[ = 1\,\,000 - 500\] \[ = 500\]. d) \[\left( { - 16} \right) \cdot 125 \cdot \left[ {\left( { - 5} \right) \cdot {2^2}} \right] \cdot {5^4} - 12 \cdot {10^6}\] \( = \left( { - {2^4}} \right) \cdot {5^3} \cdot \left[ {\left( { - 5} \right) \cdot {2^2}} \right] \cdot {5^4} - 12 \cdot {10^6}\) \( = \left( { - {2^4} \cdot {2^2}} \right) \cdot \left[ {{5^3} \cdot \left( { - 5} \right) \cdot {5^4}} \right] - 12 \cdot {10^6}\) \( = \left( { - {2^6}} \right) \cdot \left( { - {5^8}} \right) - 12 \cdot {10^6}\) \( = {2^6} \cdot {5^8} - 12 \cdot {10^6}\) \( = {2^6} \cdot {5^6} \cdot {5^2} - 12 \cdot {10^6}\) \( = {10^6} \cdot 25 - 12 \cdot {10^6}\) \[ = {10^6} \cdot \left( {25 - 12} \right)\] \( = {10^6} \cdot 13\) \( = 13\,\,000\,\,000\). |
Lời giải
Hướng dẫn giải
|
a) \[\left( {123 - 4x} \right) - 67 = 8\] \[123 - 4x = 75\] \[4x = 48\] \(x = 12\) Vậy \(x = 12.\) b) \[\left( {3x - 1} \right) + 18 = - 40\] \[3x - 1 = - 58\] \(3x = - 57\) \(x = - 19.\) Vậy \(x = - 19.\) |
c) \(3 \cdot {\left( {2x - 11} \right)^2} + 6 = {3^4}\) \(3 \cdot {\left( {2x - 11} \right)^2} = 81 - 6\) \(3 \cdot {\left( {2x - 11} \right)^2} = 75\) \({\left( {2x - 11} \right)^2} = 25\) |
|
Trường hợp 1: \(2x - 11 = 5\) \(2x = 16\) \(x = 8\) Vậy \(x \in \left\{ {3;\,\,8} \right\}.\) |
Trường hợp 2: \(2x - 11 = - 5\) \(2x = 6\) \(x = 3\). |
Lời giải
Hướng dẫn giải
1. Tổng số điểm của bạn Mai sau cuộc thi là:
\(10 + 5 \cdot \left( { + 30} \right) + 3 \cdot \left( { - 20} \right) = 100\) (điểm).
Tổng số điểm của bạn Nam sau cuộc thi là:
\(10 + 3 \cdot \left( { + 30} \right) + 5 \cdot \left( { - 20} \right) = 0\) (điểm).
Vậy số điểm của bạn Mai và Nam sau cuộc thi lần lượt là \(100\) điểm và \(0\) điểm.
2. Gọi \(a\) (học sinh) là số học sinh của trường THCS đó \(\left( {a \in \mathbb{N},\,\,100 \le a < 250} \right)\).
Do khi xếp hàng 10 em thì thừa 8 em nên \(a\) chia 10 dư 8, hay \(\left( {a + 2} \right) \vdots 10\).
Khi xếp hàng 12 em thì thừa 10 em nên \(a\) chia 12 dư 10, hay \(\left( {a + 2} \right) \vdots 12\).
Khi xếp hàng 15 em thì thừa 13 em nên \(a\) chia 15 dư 13, hay \(\left( {a + 2} \right) \vdots 15\).
Từ đó suy ra \(a + 2 \in {\rm{BC}}\left( {10,12,15} \right)\).
Ta có: \(10 = 2 \cdot 5\); \(12 = {2^2} \cdot 3\); \(15 = 3 \cdot 5\).
Do đó \({\rm{BCNN}}\left( {10,12,15} \right) = {2^2} \cdot 3 \cdot 5 = 60\).
Suy ra \[a + 2 \in {\rm{BC}}\left( {10,12,15} \right) = {\rm{B}}\left( {60} \right) = \left\{ {0;\,\,60;\,\,120;\,\,180;\,\,240;\,\,300;\,\,360;\,\,420;\,\,...} \right\}\]
Khi đó \[a \in \left\{ { - 2;\,\,58;\,\,118;\,\,178;\,\,238;\,\,298;\,\,358;\,\,418;\,\,...} \right\}\]
Mà \(100 \le a < 250\) nên \(a \in \left\{ {118;\,\,178;\,\,238} \right\}\)
Mặt khác khi số học sinh của trường xếp hàng 17 thì vừa đủ nên \(a\,\, \vdots \,\,17\)
Xét 3 trường hợp ở trên ta có \(a = 238\) thỏa mãn.
Vậy trường THCS đó có 238 học sinh.
</></>
Lời giải
Hướng dẫn giải
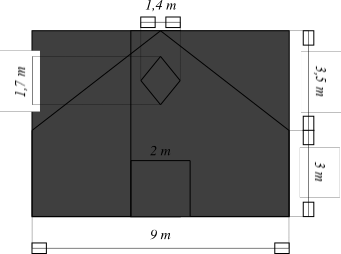
a) Công thức tính diện tích hình tam giác khi biết độ dài cạnh đáy \(a\) và chiều cao \(h\) tương ứng là:
\(\frac{1}{2}ah\) (đơn vị diện tích).
b) Diện tích cửa đi hình chữ nhật là:
Diện tích cửa thoáng hình thoi là: \(2 \cdot 2 = 4{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)\(\frac{1}{2} \cdot 1,7 \cdot 1,4 = 1,19{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
c) Diện tích của phần bức tường hình chữ nhật (không tính cửa đi) là:
\(9 \cdot 3 - 4 = 23{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích của phần bức tường hình tam giác (không tính cửa thoáng hình thoi) là:
\(\frac{1}{2} \cdot 3,5 \cdot 9 - 1,19 = 14,56{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Phần diện tích của bức tường cần sơn là:
\(23 + 14,56 = 37,56{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Số tiền bác Nam phải trả để sơn bức tường là:
\(37,56 \cdot 30\,\,000 = 1\,\,126\,\,800\) (đồng).
Lời giải
Hướng dẫn giải
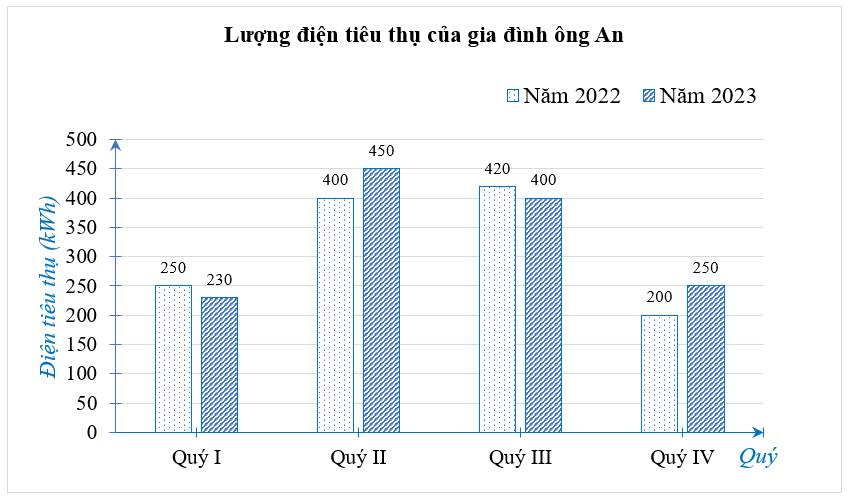
a) Trong năm 2023, quý II gia đình ông An sử dụng nhiều điện nhất.
b) Trong năm 2022 gia đình ông An tiêu thụ số kWh điện là:
\(250 + 400 + 420 + 200 = 1\,\,270\) (kWh).
c) Trong năm 2023 gia đình ông An tiêu thụ số kWh điện là:
\(230 + 450 + 400 + 250 = 1\,\,330\) (kWh).
Năm 2023 ông An tiêu thụ số kWh điện nhiều hơn năm 2022 là:
\(1\,\,330 - 1\,\,270 = 60\) (kWh).
Năm 2023 gia đình ông An phải trả nhiều hơn năm 2022 số tiền là:
\(60 \cdot 2\,\,461 = 147\,\,660\) (đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo