5 câu Trắc nghiệm Tính chất ba đường cao của tam giác có đáp án (Nhận biết)
51 người thi tuần này 4.6 1.9 K lượt thi 5 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 2
Bộ 5 đề thi Cuối kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 3
Bộ 5 đề thi học kì 1 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 1
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
- Trong một tam giác, ba đường cao cùng đi qua một điểm, điểm này gọi là trực tâm của tam giác nên phương án A, B là đúng.
- Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó nên phương án D đúng.
- Điểm cách đều ba đỉnh của một tam giác là giao điểm ba đường trung trực của tam giác đó. Do đó phương án C là sai.
Vậy ta chọn đáp án C.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
- Tam giác nhọn có trực tâm nằm bên trong tam giác;
- Tam giác tù có trực tâm nằm bên ngoài tam giác;
- Tam giác vuông có trực tâm trùng với đỉnh góc vuông.
Vậy cả 3 phát biểu đều đúng, ta chọn phương án D.
Câu 3
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
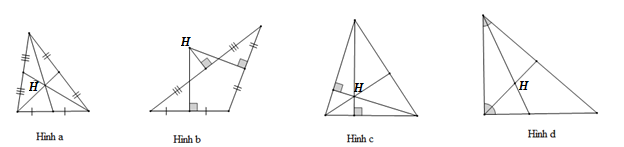
Đoạn thẳng vuông góc kẻ từ một đỉnh của một tam giác đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó nên điểm H là giao điểm của ba đường cao trong tam giác ở Hình c.
Vậy ta chọn phương án C.
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
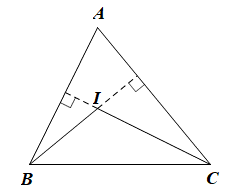
Xét DIBC có: CA ⊥ BI và BA ⊥ CI nên CA và BA là hai đường cao của tam giác IBC.
Mà hai đường thẳng CA và BA cắt nhau tại A
Do đó A là trực tâm của tam giác IBC.
Vậy ta chọn phương án A.
Câu 5
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
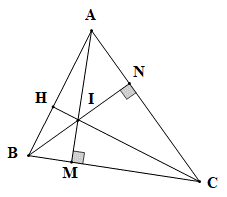
Xét DABC có hai đường cao AM và BN cắt nhau tại I nên I là trực tâm tam giác ABC.
Suy ra CI là đường cao của tam giác ABC hay CI ⊥ AB.
Do đó phương án A là đúng.
Vậy ta chọn phương án A.