Bộ 10 đề thi Giữa kì 2 Toán 9 Cánh diều cấu trúc mới có đáp án - Đề 06
18 người thi tuần này 4.6 1.9 K lượt thi 4 câu hỏi 45 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
Dạng 1: Giải hệ phương trình bằng phương pháp đặt ẩn phụ
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
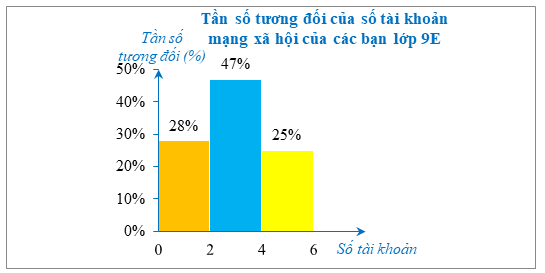
a) Đối tượng thống kê là số tài khoản mạng xã hội của các bạn lớp 9E.
Tiêu chí thống kê là tầm số tương đối của số tài khoản mạng xã hội của các bạn lớp 9E.
b) Quan sát biểu đồ, ta thấy số mạng tài khoản xã hội chiếm tần số tương đối cao nhất là nhóm \(\left[ {2;4} \right)\) tức là hoặc lớn hơn bằng \(2\) và nhỏ hơn \(4,\) chiếm \(47\% \).
Nhóm \(\left[ {4;6} \right)\) là nhóm có tần số tương đối thấp nhất, chiếm \(25\% \).
c) Ta có bảng tần số tương đối như sau:
|
Số tài khoản |
\(\left[ {0;2} \right)\) |
\(\left[ {2;4} \right)\) |
\(\left[ {4;6} \right)\) |
|
Tần số tương đối(%) |
28% |
47% |
25% |
d) Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng như sau:
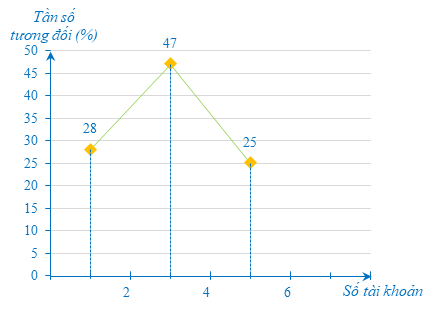
Tổng tần số tương đối của hai nhóm \(\left[ {2;\,\,4} \right)\) và \(\left[ {4;\,\,6} \right)\) là: \(47\% + 25\% = 72\% > 70\% .\)
Như vậy bạn Phương nhận định đúng.
Lời giải
2.1. a) Số học sinh nam lớp 9A là: \(2 + 1 + 2 + 1 + 1 + 1 + 2 + 2 + 2 + 2 = 16\) (học sinh).
Số học sinh nữ lớp 9A là: \(1 + 2 + 1 + 1 + 2 + 2 + 2 + 1 + 1 + 1 = 14\) (học sinh).
Số học sinh của lớp 9A là: \(16 + 14 = 30\) (học sinh)
b) Quan sát bảng số liệu, số lượng học sinh sinh tháng 10 là \(2\) học sinh.
Suy ra xác suất để chọn được bạn nam sinh tháng 10 là \(\frac{2}{{30}} = \frac{1}{{15}}\) .
c) Số học sinh sinh từ tháng 8 đến tháng 12 là: \(2 + 1 + 1 + 1 = 5\) (học sinh)
Suy ra xác suất chọn được bạn nữ sinh từ tháng 8 đến tháng 12 là: \(\frac{5}{{14}}\).
2.2 a) Kí hiệu \(\left( {i;\,\,j} \right)\) là kết quả của phép thử, trong đó \(i,\,\,j\) tương ứng là hai số trên thẻ được lấy ra ở lần thứ nhất và lần thứ hai.
Ta liệt kê tất cả kết quả của phép thử bằng cách lập bảng sau:
|
Lần 1 Lần 2 |
\( - 2\) |
\( - 1\) |
\(2\) |
\(4\) |
|
\( - 2\) |
\(\left( { - 2,\,\, - 2} \right)\) |
\(\left( { - 1,\,\, - 2} \right)\) |
\(\left( {2,\,\, - 2} \right)\) |
\(\left( {4,\,\, - 2} \right)\) |
|
\[ - 1\] |
\(\left( { - 2,\,\, - 1} \right)\) |
\(\left( { - 1,\,\, - 1} \right)\) |
\(\left( {2,\,\, - 1} \right)\) |
\(\left( {4,\,\, - 1} \right)\) |
|
\(2\) |
\(\left( { - 2,\,\,2} \right)\) |
\(\left( { - 1,\,\,2} \right)\) |
\(\left( {2,\,\,2} \right)\) |
\(\left( {4,\,\,2} \right)\) |
|
\(4\) |
\(\left( { - 2,\,\,4} \right)\) |
\(\left( { - 1,\,\,4} \right)\) |
\(\left( {2,\,\,4} \right)\) |
\(\left( {4,\,\,4} \right)\) |
Không gian mẫu của phép thử là:
\(\Omega = \left\{ {\left( { - 2,\,\, - 2} \right);\,\,\left( { - 1,\,\, - 2} \right);\,\,\left( {2,\,\, - 2} \right);\,\,\left( {4,\,\, - 2} \right);\,\,\left( { - 2,\,\, - 1} \right);\,\,\left( { - 1,\,\, - 1} \right);\,\,\left( {2,\,\, - 1} \right);\,\,} \right.\left( {4,\,\, - 1} \right);\,\)
\(\left( { - 2,\,\,2} \right);\,\,\left( { - 1,\,\,2} \right);\)\(\left. {\left( {2,\,\,2} \right);\,\,\left( {4,\,\,2} \right);\,\,\left( { - 2,\,\,4} \right);\,\,\left( { - 1,\,\,4} \right);\,\,\left( {2,\,\,4} \right);\,\,\left( {4,\,\,4} \right)} \right\}.\)
Không gian mẫu có 16 phần tử.
b) Vì các thẻ số có cùng kích thước và vật liệu nên các kết quả của phép thử là đồng khả năng.
Các kết quả thuận lợi cho biến cố đã cho là:
\(\left( {4,\,\, - 2} \right);\,\,\left( {2,\,\, - 1} \right);\,\,\left( {4,\,\, - 1} \right);\,\,\left( { - 1,\,\,2} \right);\,\,\left( {2,\,\,2} \right);\,\,\left( {4,\,\,2} \right);\,\,\left( { - 2,\,\,4} \right);\,\,\left( { - 1,\,\,4} \right);\,\,\left( {2,\,\,4} \right);\,\,\left( {4,\,\,4} \right).\)
Có 10 kết quả thuận lợi cho biến cố đã cho.
Vậy xác suất của biến cố đã cho là: \(\frac{{10}}{{16}} = \frac{5}{8}.\)
Lời giải
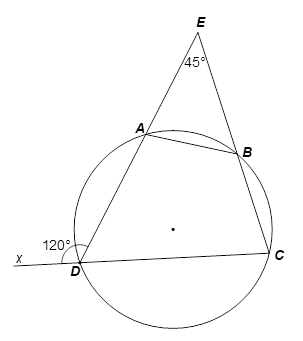
3.1. Ta có \(\widehat {ADx} + \widehat {ADC} = 180^\circ \) (hai góc kề bù)
Tứ giác \(ABCD\) nội tiếp đường tròn nên \(\widehat {ABC} + \widehat {ADC} = 180^\circ \) (tổng hai góc đối nhau trong một tứ giác nội tiếp). Suy ra \(\widehat {ABC} = \widehat {ADx} = 120^\circ .\)
Mà \(\widehat {ABC}\) là góc ngoài tại đỉnh \(B\) của tam giác \(ABE\) nên \(\widehat {ABC} = \widehat {AEB} + \widehat {BAE}\).
Suy ra \(\widehat {BAE} = \widehat {ABC} - \widehat {AEB} = 120^\circ - 45^\circ = 75^\circ .\)
Lại có \(\widehat {BAE} + \widehat {BAD} = 180^\circ \) (hai góc kề bù) và \(\widehat {BCD} + \widehat {BAD} = 180^\circ \) (tổng hai góc đối nhau trong tứ giác \(ABCD\) nội tiếp).
Suy ra \(\widehat {BCD} = \widehat {BAE} = 75^\circ .\)
|
3.2. Gọi \[H\] là hình chiếu của \[A\] trên \[Oy.\] Ta có \(A\left( {3;\,\,3} \right)\) nên \(OH = AH = \left| 3 \right| = 3.\) Xét \[\Delta AOH\] vuông tại \[H,\] theo định lí Pythagore ta có: \[O{A^2} = O{H^2} + A{H^2}\] Suy ra \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{3^2} + {3^2}} = \sqrt {18} = 3\sqrt 2 .\) |
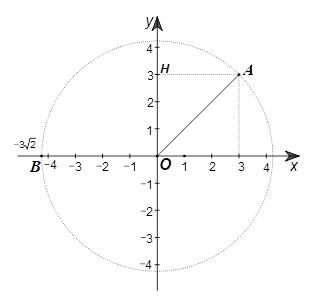 |
Ta cũng có \(\sin \widehat {AOH} = \frac{{AH}}{{OA}} = \frac{3}{{3\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.\) Suy ra \(\widehat {AOH} = 45^\circ .\)
Ta có điểm \(B\left( { - 3\sqrt 2 ;\,\,0} \right)\) nằm trên trục \[Ox\] nên \(OB = \left| { - 3\sqrt 2 } \right| = 3\sqrt 2 .\)
Khi đó \(OA = OB = 3\sqrt 2 .\)
Mặt khác, \(\widehat {AOB} = \widehat {AOH} + \widehat {HOB} = 45^\circ + 90^\circ = 135^\circ .\)
Như vậy, phép quay \(135^\circ \) ngược chiều kim đồng hồ quanh gốc tọa độ biến điểm \(A\) thành điểm \(B\).
Lời giải
|
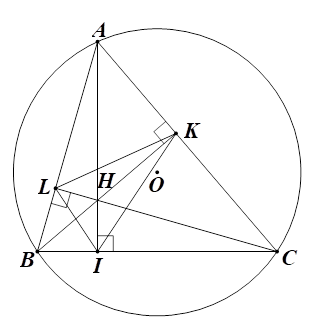
a) Vì \(AI,\,\,CL\) là đường cao của tam giác \(ABC\) nên \(AI \bot BC\) và \(CL \bot AB.\) Do đó \(\widehat {AIB} = \widehat {BLC} = 90^\circ \) hay \(\widehat {HIB} = \widehat {BLH} = 90^\circ \). Suy ra hai điểm \(I,\,\,L\) cùng nằm trên đường tròn đường kính \(BH.\) Vậy bốn điểm \(B,\,\,I,\,\,L,\,\,H\) cùng nằm trên đường tròn đường kính \(BH\) hay tứ giác \(BIHL\) nội tiếp đường tròn đường kính \(BH.\) b) Chứng minh tương tự câu 1, ta có tứ giác \(CIHK\) nội tiếp đường tròn đường kính \(CH.\) Suy ra \(\widehat {IKC} = \widehat {IHC}\) (hai góc nội tiếp cùng chắn cung \(IC)\) |
 |
Chứng minh tương tự, ta có tứ giác \(AKHL\) nội tiếp đường tròn đường kính \(AH\) nên \(\widehat {AKL} = \widehat {AHL}\) (hai góc nội tiếp cùng chắn cung \(AL).\)
Lại có \(\widehat {IHC} = \widehat {AHL}\) (đối đỉnh)
Do đó \(\widehat {AKL} = \widehat {IKC}.\)
Ta có \(\widehat {AKL} + \widehat {LKB} = 90^\circ \) và \(\widehat {IKC} + \widehat {IKB} = 90^\circ \)
Mà \(\widehat {AKL} = \widehat {IKC}\) nên \(\widehat {LKB} = \widehat {IKB}\) hay \(KB\) tức \(KH\) là tia phân giác của \(\widehat {IKL}.\)
Chứng minh tương tự, ta có \(IH\) là tia phân giác của \(\widehat {LIK}.\)
Xét tam giác \(IKL\) có \(KH,\,\,IH\) là hai đường phân giác của tam giác cắt nhau tại \(H\) nên \(H\) là tâm đường tròn nội tiếp tam giác \(IKL.\)