15 câu Trắc nghiệm Toán 9 Cánh diều Bài tập cuối chương I có đáp án
29 người thi tuần này 4.6 658 lượt thi 15 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
Danh sách câu hỏi:
Câu 1
A. \[x \ne 0\] và \[x \ne - 4.\]
B. \[x \ne 4.\]
C. \[x \ne 0.\]
D. \[x \ne 0\] và \[x \ne 4.\]
Lời giải
Đáp án đúng là: D
Điều kiện xác định của phương trình \[\frac{1}{x} - \frac{2}{3} = \frac{{5{x^2}}}{{x - 4}}\] là \[x \ne 0\] và \[x - 4 \ne 0.\]
Tức là, \[x \ne 0\] và \[x \ne 4.\]
Vậy ta chọn phương án D.
Câu 2
A. \[a = - 7,b = 0,c = 12.\]
B. \[a = - 7,b = - 12,c = 0.\]
C. \[a = 0,b = - 7,c = 12.\]
D. \[a = 0,b = - 12,c = 0.\]
Lời giải
Đáp án đúng là: A
Phương trình bậc nhất hai ẩn \[x,y\] là hệ thức dạng \[ax + by = c\] với \[a \ne 0\] hoặc \[b \ne 0.\]
Ta viết phương trình \[ - 7x - 12 = 0\] thành \( - 7x + 0y = 12\).
Do đó, ta có \[a = - 7,\,\,b = 0,\,\,c = 12.\]
Vậy ta chọn phương án A.
Câu 3
A. \[\left( { - 1;1} \right).\]
B. \[\left( {5;3} \right).\]
C. \[\left( {0;1} \right).\]
D. \[\left( { - 1; - 1} \right).\]
Lời giải
Đáp án đúng là: D
⦁ Thay \[x = - 1,y = 1\] vào phương trình \[3x - 2y + 1 = 0,\] ta được:
\[3 \cdot \left( { - 1} \right) - 2 \cdot 1 + 1 = - 4 \ne 0.\]
Do đó cặp số \[\left( { - 1;1} \right)\] không là nghiệm của phương trình \[3x - 2y + 1 = 0.\]
⦁ Thay \[x = 5,y = 3\] vào phương trình \[3x - 2y + 1 = 0,\] ta được:
\[3 \cdot 5 - 2 \cdot 3 + 1 = 10 \ne 0.\]
Do đó cặp số \[\left( {5;3} \right)\] không là nghiệm của phương trình \[3x - 2y + 1 = 0.\]
⦁ Thay \[x = 0,y = 1\] vào phương trình \[3x - 2y + 1 = 0,\] ta được:
\[3 \cdot 0 - 2 \cdot 1 + 1 = - 1 \ne 0.\]
Do đó cặp số \[\left( {0;1} \right)\] không là nghiệm của phương trình \[3x - 2y + 1 = 0.\]
⦁ Thay \[x = - 1,y = - 1\] vào phương trình \[3x - 2y + 1 = 0,\] ta được:
\[3 \cdot \left( { - 1} \right) - 2 \cdot \left( { - 1} \right) + 1 = 0\] (đúng).
Do đó cặp số \[\left( { - 1; - 1} \right)\] là nghiệm của phương trình \[3x - 2y + 1 = 0.\]
Vậy ta chọn phương án D.
Câu 4
A. \[a = 9,b = 10,c = 2\] và \[a' = 5,b' = - 3,c' = - 6.\]
B. \[a = 2,b = 9,c = 10\] và \[a' = - 3,b' = 5,c' = - 6.\]
C. \[a = 9,b = 2,c = - 10\] và \[a' = 5,b' = 3,c' = - 6.\]
D. \[a = 2,b = 9,c = 10\] và \[a' = - 3,b' = - 5,c' = 6.\]
Lời giải
Đáp án đúng là: B
Ta viết hệ phương trình \[\left\{ \begin{array}{l}2x + 9y = 10\\5y - 3x = - 6\end{array} \right.\] thành \[\left\{ \begin{array}{l}2x + 9y = 10\\ - 3x + 5y = - 6\end{array} \right.\] có dạng \[\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right..\]
Trong đó, \[a = 2,b = 9,c = 10\] và \[a' = - 3,b' = 5,c' = - 6.\]
Vậy ta chọn phương án B.
Câu 5
A. \[\left\{ \begin{array}{l}x - 5y = 13\\x - y = 3.\end{array} \right.\]
B. \[\left\{ \begin{array}{l}x - 5y = 13\\2x - 3y = - 1.\end{array} \right.\]
C. \[\left\{ \begin{array}{l}x - y = 6\\2x + y = - 3.\end{array} \right.\]
D. \[\left\{ \begin{array}{l}x + y = 8\\x - y = 3.\end{array} \right.\]
Lời giải
Đáp án đúng là: C
⦁ Thay \[x = 1,y = - 5\] vào phương trình \[x - 5y = 13,\] ta được: \[1 - 5 \cdot \left( { - 5} \right) = 26 \ne 13.\]
Do đó cặp số \[\left( {1; - 5} \right)\] không là nghiệm của hệ phương trình ở các phương án A, B.
⦁ Thay \[x = 1,y = - 5\] vào mỗi phương trình trong hệ ở phương án C, ta được:
\[1 - \left( { - 5} \right) = 6\] (đúng);
\[2 \cdot 1 + \left( { - 5} \right) = - 3\] (đúng).
Do đó cặp số \[\left( {1; - 5} \right)\] là nghiệm của từng phương trình trong hệ phương trình ở phương án C.
Vì vậy cặp số \[\left( {1; - 5} \right)\] là nghiệm của hệ phương trình ở phương án C.
⦁ Thay \[x = 1,y = - 5\] vào phương trình \[x + y = 8,\] ta được: \[1 + \left( { - 5} \right) = - 4 \ne 8\]
Do đó cặp số \[\left( {1; - 5} \right)\] không là nghiệm của hệ phương trình ở phương án D.
Vậy ta chọn phương án C.
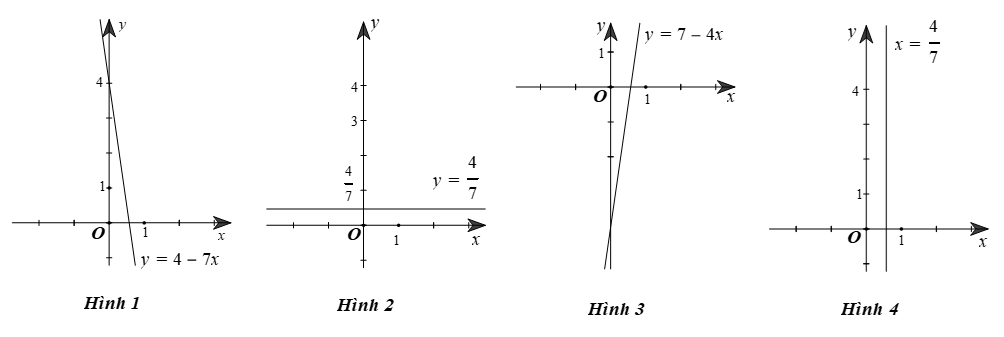
Câu 6
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[3x + y = - 4.\]
B. \[3x - y = - 1.\]
C. \[3x - y = 5.\]
D. \[3x + y = 6.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. \[{x_0} = 7.\]
B. \[{x_0} = - 1.\]
C. \[{x_0} = - 2.\]
D. \[{x_0} = 2.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. \[x = 3\] và \[x = 2.\]
B. \[x = - 3\] và \[x = - 2.\]
C. \[x = 3.\]
D. \[x = - 2.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \[ - 6y = - 21.\]
B. \[y = - 3y - 2.\]
C. \[ - 6y = - 1.\]
D. \[6y = - 1.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A. \[\left( {x;y} \right) = \left( {2;3} \right).\]
B. \[\left( {x;y} \right) = \left( {2; - 3} \right).\]
C. \[\left( {x;y} \right) = \left( { - 2; - 3} \right).\]
D. \[\left( {x;y} \right) = \left( { - 2;3} \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. \[x = - 5.\]
B. \[x = 5.\]
C. \[x = 2.\]
D. \[x = - 1.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
A. \[m = 3.\]
B. \[m = - 3.\]
C. \[m = 7.\]
D. \[m = 7\] hoặc \[m = - 3.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. \[200\] và \[300.\]
B. \[250\] và \[250.\]
C. \[300\] và \[200.\]
D. \[400\] và \[100.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.