Bộ 10 đề thi Giữa kì 2 Toán 9 Cánh diều cấu trúc mới có đáp án - Đề 07

     a) Có 5 giá trị khác nhau của số bàn thắng được ghi lại, đó là: \[0;1;2;3;4\].

     b) Từ số liệu trên, có 26 trận đấu của Giải vô địch quốc gia.

     c) Ta có bảng tần số cho mẫu số liệu trên như sau:

     d) Trong 26 số liệu thống kê có 5 giá trị khác nhau là:

\[{x_1} = 0;{\rm{ }}{x_2} = 1;{\rm{ }}{x_3} = 2;{\rm{ }}{x_4} = 3;{\rm{ }}{x_5} = 4.\]

Các giá trị \[{x_1},{\rm{ }}{x_2},{\rm{ }}{x_3},{\rm{ }}{x_4},{\rm{ }}{x_5}\] lần lượt có tần số là:

\[{n_1} = 10;{\rm{ }}{n_2} = 3;{\rm{ }}{n_3} = 3;{\rm{ }}{n_4} = 8;{\rm{ }}{n_5} = 2.\]

Các giá trị \[{x_1},{\rm{ }}{x_2},{\rm{ }}{x_3},{\rm{ }}{x_4},{\rm{ }}{x_5}\] lần lượt có tần số tương đối là:

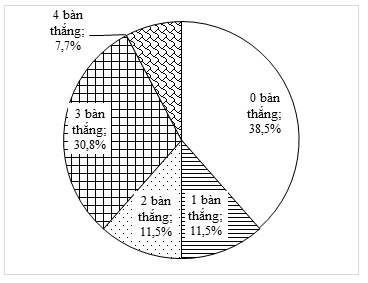
\[{f_1} = \frac{{10 \cdot 100}}{{26}}\%  \approx 38,5\% ;\] \[{f_2} = \frac{{3 \cdot 100}}{{26}}\%  \approx 11,5\% ;\] \[{f_3} = \frac{{3 \cdot 100}}{{26}}\%  \approx 11,5\% ;\]

\[{f_4} = \frac{{8 \cdot 100}}{{26}}\%  \approx 30,8\% ;\] \[{f_5} = \frac{{2 \cdot 100}}{{26}}\%  \approx 7,7\% .\]

Bảng tần số tương đối của mẫu số liệu thống kê đó như sau:

Biểu đồ tần số tương đối hình quạt tròn của mẫu số liệu thống kê đó như sau:

     2.1. a) Số học sinh nữ tham gia câu lạc bộ là: \(1 + 2 + 3 + 4 + 5 + 6 + 3 + 2 = 26\) (học sinh)

               Số học sinh nam tham gia câu lạc bộ là: \(5 + 3 + 4 + 2 + 3 + 1 + 2 + 4 = 24\) (học sinh)

               Số học sinh tham gia câu lạc bộ của lớp 9B là: \(26 + 24 = 50\) (học sinh)

     b) Từ bảng số liệu, số học sinh tham gia câu lạc bộ Âm nhạc là \(8\) học sinh.

         Xác suất để chọn được bạn tham gia câu lạc bộ Âm Nhạc là: \(\frac{8}{{50}} = \frac{2}{{25}}\).

     c) Từ bảng số liệu, số học sinh nữ tham gia câu lạc bộ Cờ Vua hoặc Văn học là: \(10\) bạn.

         Do đó, xác suất để chọn được một bạn nữ tham gia câu lạc bộ Cờ vua hoặc Văn học là: \(\frac{{10}}{{50}} = \frac{1}{5}.\)

     2.2. a) Xét phép thử “Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng”.

Ta thấy, các kết quả xảy ra của phép thử đó là đồng khả năng.

Kết quả xảy ra của phép thử là một bộ ba \[(a\] cm, \[b\] cm, \[c\] cm), trong đó \[a\] cm, \[b\] cm và \[c\] cm tương ứng là độ dài của ba đoạn thẳng được lấy ra. Do ba đoạn thẳng được lấy ra cùng một lúc nên \[a,{\rm{ }}b\] và \[c\] đôi một khác nhau.

Tập hợp các kết quả của phép thử là:

\[\Omega  = \left\{ {\left( {1{\rm{\;cm}},{\rm{ 3\;cm}},{\rm{ 5\;cm}}} \right);} \right.\]\[\left( {1{\rm{\;cm}},{\rm{ 3\;cm}},{\rm{ 7\;cm}}} \right);\]\[\left( {1{\rm{\;cm}},{\rm{ 3\;cm}},{\rm{ 9\;cm}}} \right);\]\[\left( {1{\rm{\;cm}},{\rm{ 5\;cm}},{\rm{ 7\;cm}}} \right);\] \[\left( {1{\rm{\;cm}},{\rm{ 5\;cm}},{\rm{ 9\;cm}}} \right);\] \[\left( {1{\rm{\;cm}},{\rm{ 7\;cm}},{\rm{ 9\;cm}}} \right);\] \[\left( {3{\rm{\;cm}},{\rm{ 5\;cm}},{\rm{ 7\;cm}}} \right);\] \[\left( {3{\rm{\;cm}},{\rm{ 5\;cm}},{\rm{ 9\;cm}}} \right);\] \[\left( {3{\rm{\;cm}},{\rm{ 7\;cm}},{\rm{ 9\;cm}}} \right);\] \[\left. {\left( {5{\rm{\;cm}},{\rm{ 7\;cm}},{\rm{ 9\;cm}}} \right)} \right\}.\]

Tập hợp \[\Omega \] có 10 phần tử.

     b) Ta có: \(7 < 3 + 5;\,\,9 < 3 + 7;\,\,9 < 5 + 7\) nên ba bộ ba các đoạn thẳng lập thành ba cạnh của một tam giác là: \[\left( {3{\rm{\;cm}},{\rm{ 5\;cm}},{\rm{ 7\;cm}}} \right);\] \[\left( {3{\rm{\;cm}},{\rm{ 7\;cm}},{\rm{ 9\;cm}}} \right);\] \[\left( {5{\rm{\;cm}},{\rm{ 7\;cm}},{\rm{ 9\;cm}}} \right).\]

Do đó có 3 kết quả thuận lợi cho biến cố đã cho.

Vậy xác suất của biến cố đó là: \(\frac{3}{{10}}.\)

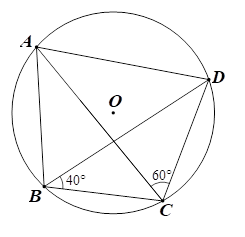
       3.1. Xét đường tròn \(\left( O \right),\) ta có \(\widehat {ABD} = \widehat {ACD} = 60^\circ \) (hai góc nội tiếp cùng chắn cung \(AD)\)

Tứ giác \(ABCD\) nội tiếp đường tròn nên \(\widehat {ADC} + \widehat {ABC} = 180^\circ \).

Suy ra \[\widehat {ADC} = 180^\circ  - \widehat {ABC} = 180^\circ  - \left( {\widehat {ABD} + \widehat {DBC}} \right) = 180^\circ  - \left( {60^\circ  + 40^\circ } \right) = 80^\circ .\]    

3.2.

Xét \(\Delta ABC\) đều có \(AB = AC\) và \(\widehat {BAC} = 60^\circ \).

Phép quay thuận chiều kim đồng hồ với tâm \(A\) biến điểm \(B\) thành điểm \(C\) tạo nên cung lớn \(BC\) có số đo là:

$360°-\text{sđ}\stackrel{⏜}{BC}=360°-\widehat{BAC}=360°-60°=300°.$

Vậy góc quay của phép quay đó là \(300^\circ .\)

a) Vì \(F,\,\,E\) là tiếp điểm của đường tròn \(\left( I \right)\) nội tiếp tam giác \(ABC\) nên \[IF \bot AB,\,\,IE \bot AC.\]

Do đó \(\widehat {IFA} = \widehat {IEA} = 90^\circ \), nên hai tam giác \(AIF,\,\,AIE\) là hai tam giác vuông có cùng cạnh huyền \(AI\)

Do đó đường tròn ngoại tiếp hai tam giác \(AIF,\,\,AIE\) là đường tròn đường kính \(AI\) hay bốn điểm \(A,\,\,E,\,\,I,\,\,F\) cùng nằm trên đường tròn đường kính \(AI.\)

Vậy tứ giác \(AEIF\) là tứ giác nội tiếp.

b) Đường tròn tâm \(I\) nội tiếp tam giác \(ABC\) nên \(AI,\,\,BI,\,\,CI\) là các đường phân giác của tam giác.

Do đó \(\widehat {IAF} = \frac{1}{2}\widehat {BAC};\,\,\widehat {IBC} = \frac{1}{2}\widehat {ABC};\,\,\widehat {ICB} = \frac{1}{2}\widehat {ACB}\).

Ta có: \(\widehat {AIF} = 90^\circ  - \widehat {IAF} = 90^\circ  - \frac{1}{2}\widehat {BAC}\). (1)

\[\widehat {IBC} + \widehat {ICB} = \frac{1}{2}\widehat {ABC} + \frac{1}{2}\widehat {ACB} = \frac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right) = \frac{1}{2}\left( {180^\circ  - \widehat {BAC}} \right) = 90^\circ  - \frac{1}{2}\widehat {BAC}.\] (2)

Xét \(\Delta IBC\) có \(\widehat {KIC}\) là góc ngoài tại đỉnh \(I\) nên \(\widehat {KIC} = \widehat {IBC} + \widehat {ICB}.\) (3)

Từ (1), (2) và (3) suy ra \(\widehat {AIF} = \widehat {KIC}.\) (4)

Tứ giác \(AEIF\) là tứ giác nội tiếp nên \(\widehat {AEF} = \widehat {AIF}\) (hai góc nội tiếp cùng chắn cung \(AF).\) (5)

Chứng minh tương tự câu 1, ta có tứ giác \(IEKC\) nội tiếp đường tròn đường kính \(IC.\)

Do đó \(\widehat {KEC} = \widehat {KIC}\) (hai góc nội tiếp cùng chắn cung \(KC).\) (6)

Từ (4), (5), (6) ta có \(\widehat {AEF} = \widehat {KEC}\).

Mà \(\widehat {AEF} + \widehat {FEC} = 180^\circ \) nên \(\widehat {KEC} + \widehat {FEC} = 180^\circ \) hay ba điểm \(F,\,\,E,\,\,K\) thẳng hàng.