Bộ 15 đề thi ôn vào lớp 6 môn Toán chất lượng cao năm 2024 - 2025 có đáp án (Đề 3)
24 người thi tuần này 4.6 7.6 K lượt thi 16 câu hỏi 60 phút
🔥 Đề thi HOT:
Bài tập cuối tuần Toán lớp 5 KNTT Tuần 11 có đáp án
Bài tập cuối tuần Toán lớp 5 KNTT Tuần 13 có đáp án
Bài tập cuối tuần Toán lớp 5 KNTT Tuần 14 có đáp án
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
50 cm2 × 8 + 6 dm2 = 400 cm2 + 6 dm2 = 4 dm2 + 6 dm2 = 10 dm2
Đáp số: 10
Lời giải
Ta có:
0,36 × 4 + 36% × 2 + 2 × 4 × 0,18
= 0,36 × 4 + 0,36 × 2 + 0,36 × 4
= 0,36 × (4 + 2 + 4)
= 0,36 × 10
= 3,6
Đáp số: 3,6
Lời giải
1 người trong 1 ngày làm được số mét vải là:
180 : 3 : 5 = 12 (m).
7 người trong 2 ngày thì làm được số mét vải là:
12 × 7 × 2 = 168 (m)
Đáp số: 168 mét
Lời giải
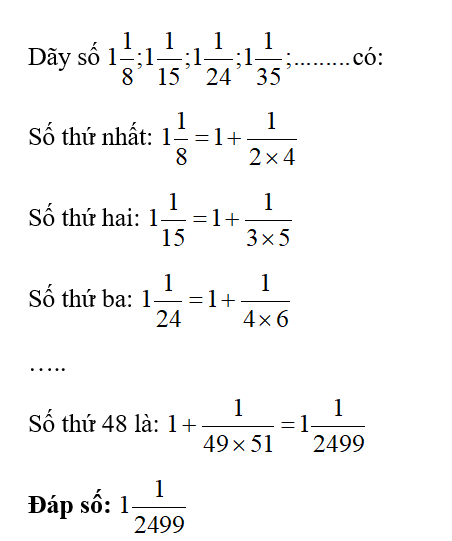
Lời giải
Tổng khối lượng của 5 bao gạo là:
40 + 48 + 60 + 44 + 25 = 217 (kg)
Sau khi lấy ra 1 bao gạo nếp thì lúc này số gạo tẻ gấp 3 lần số gạo nếp, tổng số gạo tẻ và gạo nếp là 4 phần. Suy ra tổng số gạo còn lại là một số chia hết cho 4.
Vi 217 : 4 = 54 (dư 1) nên số gạo nếp lấy ra phải là một số chia 4 dư 1.
Do đó, bao gạo nếp lấy ra nặng 25 ki-lô-gam.
Tổng số gạo còn lại sau khi lấy ra là:
217 – 25 = 192 (kg)
Lúc sau có số ki-lô-gam gạo nếp là:
192 : 4 × 1 = 48 (kg)
Lúc đầu có số ki-lô-gam gạo nếp là:
48 + 25 = 73 (kg)
Đáp số: 73 ki-lô-gam gạo nếp
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.