Bộ 10 đề thi Giữa kì 2 Toán 7 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 7
21 người thi tuần này 4.6 4.4 K lượt thi 5 câu hỏi 60 phút
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
5 câu Trắc nghiệm Tập hợp các số hữu tỉ có đáp án (Nhận biết)
6 câu Trắc nghiệm Toán 7 Bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh có đáp án (Vận dụng)
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
Bộ 5 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
8 câu Trắc nghiệm Toán 7 Bài 4: Đơn thức đồng dạng có đáp án (Nhận biết)
5 câu Trắc nghiệm Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu có đáp án (Nhận biết)
5 câu Trắc nghiệm Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng có đáp án (Nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
a) \(\frac{x}{3} = \frac{{2,5}}{{1,5}}\) suy ra \(1,5x = 2,5.3\), do đó \(x = \frac{{2,5.3}}{{1,5}} = 5\).
Vậy \(x = 5\).
b) \(\frac{x}{{15}} = \frac{y}{7}\) và \(y - x = 16\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{15}} = \frac{y}{7} = \frac{{y - x}}{{7 - 15}} = \frac{{16}}{{ - 8}} = - 2\).
Suy ra \(x = 15.\left( { - 2} \right) = - 30\) và \(y = 7.\left( { - 2} \right) = - 14\).
Vậy \(x = - 30\) và \(y = - 14\).
c) \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\) và \(x - 2y + 3z = 38.\)
Ta có \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\) hay \(\frac{x}{2} = \frac{{2y}}{6} = \frac{{3z}}{{15}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2} = \frac{{2y}}{6} = \frac{{3z}}{{15}} = \frac{{x - 2y + 3z}}{{2 + 6 + 15}} = \frac{{38}}{{23}}\).
Suy ra \(x = \frac{{76}}{{23}};y = \frac{{119}}{{23}};z = \frac{{190}}{{23}}\).
Lời giải
Hướng dẫn giải
a) Vì \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch và từ bảng trên có \(x = - 2\) thì \(y = - 15\).
Từ đây, ta có: \(a = xy = - 2.\left( { - 15} \right) = 30\). Suy ra \(y = \frac{{30}}{x}\).
Do đó, hệ số tỉ lệ của \(y\) đối với \(x\) là \(30\).
b) Ta có \(a = 30\) nên ta được bảng sau:

Lời giải
Hướng dẫn giải
3.1. Gọi thời gian để hoàn thành công việc của \(40\) công nhân là \(t\) giờ \(\left( {t > 0} \right)\).
Vì khối lượng công việc là không đổi nên số công nhân và thời gian để hoàn thành công việc đó là hai đại lượng tỉ lệ nghịch, ta có: \(30.8 = 40t\) suy ra \(t = \frac{{30.8}}{{40}} = 6\).
Vậy thời gian để hoàn thành công việc của 40 công nhân là 6 giờ.
3.2. Gọi số gạo mỗi bạn Long, Khang, My quyên góp lần lượt là \(x,y,z{\rm{ }}\left( {x,y,z > 0;{\rm{ kg}}} \right)\).
Theo đề, ta có tổng số gạo ba bạn quyên góp là \(72{\rm{ kg}}\) nên \(x + y + z = 72\) (1)
Vì số gạo ba bạn Long, Khang, My quyên góp lần lượt tỉ lệ thuận với \(5;6;7\) nên \(\frac{x}{5} = \frac{y}{6} = \frac{z}{7}\) (2)
Từ (1) và (2) áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{5} = \frac{y}{6} = \frac{z}{7} = \frac{{x + y + z}}{{5 + 6 + 7}} = \frac{{72}}{{18}} = 4\)
Suy ra \(x = 20;y = 24;z = 28\) (thỏa mãn)
Vậy số gạo ba bạn Long, Khang, My góp lần lượt là 20 kg, 24 kg, 28 kg.
Lời giải
Hướng dẫn giải
Nhận thấy trên cùng một đoạn đường, vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.
Gọi \(x,y,z,t\) lần lượt là thời gian để vật chuyển động trên 4 cạnh của hình vuông.
Theo đề, ta có: \(x + y + z + t = 130\) (1)
Lại có, trên hai cạnh đầu, vật chuyển động với vận tốc \(6{\rm{ m/s}}\), trên cạnh thứ ba với bận tốc \(4{\rm{ m/s}}\) và trên cạnh thứ tư với vận tốc \(2{\rm{ m/s}}\) nên ta có: \(6x = 6y = 4z = 2t\) (= độ dài hình vuông)
Hay \(\frac{x}{2} = \frac{y}{2} = \frac{z}{3} = \frac{t}{6}\) (2)
Từ (1) và (2) áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2} = \frac{y}{2} = \frac{z}{3} = \frac{t}{6} = \frac{{x + y + z + t}}{{2 + 2 + 3 + 6}} = \frac{{130}}{{13}} = 10\).
Suy ra \(x = y = 20;{\rm{ }}z = 30;{\rm{ }}t = 60\).
Do đó, độ dài cạnh hình vuông đó là: \(6.20 = 120{\rm{ m}}\).
Lời giải
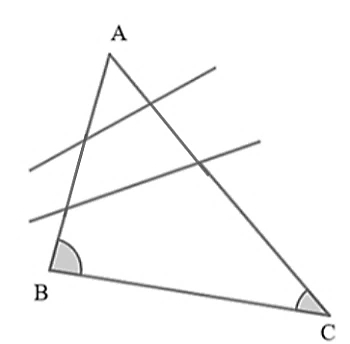
4.1. Từ hình minh họa, xét tam giác \(ABC\), có \(\widehat B > \widehat C{\rm{ }}\left( {75^\circ > 35^\circ } \right)\) nên \(AC > AB\) (quan hệ giữa góc và cạnh đối diện trong tam giác).
Do đó, bạn Đào đi đến nhà bạn Lan ngắn hơn quãng đường bạn Đào đi đến nhà bạn Hồng.
Vậy các bạn nên học nhóm ở nhà bạn Lan.
4.2. a) Xét \(\Delta AMB\) và \(\Delta AMC\), có:
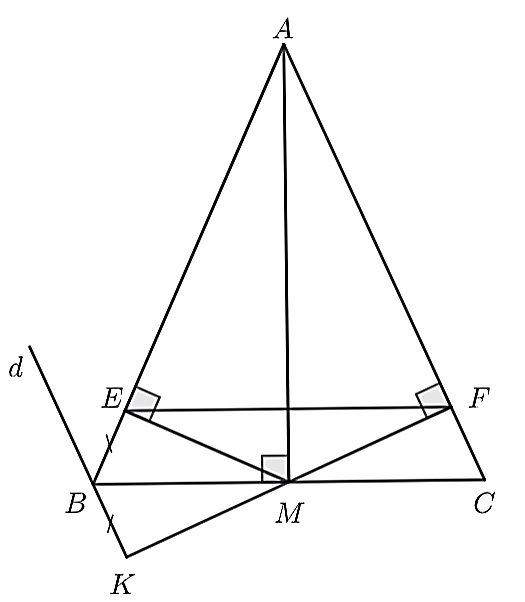
\(AM\) chung (gt)
\(BM = MC\) (gt)
\(AB = AC\) (\(\Delta ABC\) cân)
Do đó, \(\Delta AMB = \Delta AMC\) (c.c.c)
Suy ra \(\widehat {MAB} = \widehat {MAC}\) (hai cạnh tương ứng)
Do đó, \(AM\) là tia phân giác của \(\widehat {BAC}\).
b) Xét \(\Delta AME\) và \(\Delta AMF\), có:
\(\widehat {MEA} = \widehat {MFA} = 90^\circ \) (gt)
\(\widehat {EAM} = \widehat {FAM}\)
\(AM\) chung (gt)
Do đó, \(\Delta AME = \Delta AMF\) (ch – gn)
Suy ra \(ME = MF\) (hai cạnh tương ứng)
Từ đó, ta có: \(\Delta MEF\) cân tại \(M\).
c) Vì \(\Delta AME = \Delta AMF\) (cmt) nên \(AE = AF\) (hai cạnh tương ứng).
Mà \(AB = AC\) và ta có: \(\left\{ \begin{array}{l}AB = AE + EB\\AC = AF + FC\end{array} \right.\) suy ra \(EB = FC\).
Lại có \(EB = KB\) nên \(KB = FC\).
Xét \(\Delta BKM\) và \(\Delta CFM\), có:
\(BM = MC\) (gt)
\(\widehat {FCM} = \widehat {MBK}\) (so le trong)
\(KB = FC\) (cmt)
Do đó, \(\Delta BKM = \Delta CFM\) (c.g.c)
Suy ra \(\widehat {BMK} = \widehat {CMF}\) (hai góc tương ứng)
Mà hai góc ở vị trí đối đỉnh nên \(K,M,F\) thẳng hàng.
Lại có \(KM = MF\) (hai cạnh tương ứng)
Do đó, \(M\) là trung điểm của \(KF\).