Bộ 12 đề thi học kì 2 Toán 7 Cánh Diều cấu trúc mới có đáp án - Đề 11

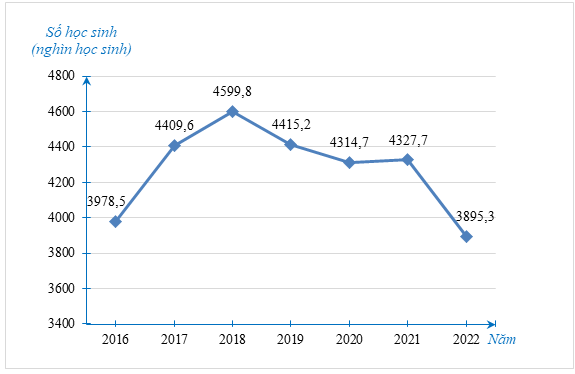
a) Bảng số liệu thống kê số học sinh mẫu giáo của nước ta như sau:

b) Trong giai đoạn từ năm 2016 đến năm 2022, năm 2022 có số học sinh mẫu giáo ít nhất.

Số học sinh mẫu giáo năm 2022 đó giảm \(4327,7 - 3895,3 = 432,4\) (nghìn học sinh), tương ứng giảm \(\frac{{432,4}}{{4327,7}}.100\%  \approx 10\% \) so với năm 2021.

c) Trong 7 năm từ năm 2016 đến năm 2022, có 3 năm có số học sinh mẫu giáo nhiều hơn \(4,4\) triệu học sinh (nhiều hơn \(4\,400\) nghìn học sinh) là năm \(2017;2018;2019\).

Xác suất để năm được chọn có số học sinh mẫu giáo nhiều hơn \(4,4\) triệu học sinh là \(\frac{3}{7}\).

a) Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra là:

         \(M = \left\{ {5;6;7;....;23;24} \right\}\).

Do đó, có 20 kết quả có thể xảy ra.

b) Các kết quả thuận lợi cho biến cố \(N\) là: \(5;7;9;....;21;23.\)

Do đó, có \(\left( {23 - 5} \right):2 + 1 = 10\) kết quả thuận lợi cho biến cố này.

Vậy xác suất của biến cố \(N\) là \(\frac{{10}}{{20}} = \frac{1}{2}\).

c) Các kết quả thuận lợi cho biến cố \(P\) là: \(6;8;12;16;24\).

Do đó, có 5 kết quả thuận lợi cho biến cố này.

Vậy xác suất của biến cố \(P\) là \(\frac{5}{{20}} = \frac{1}{4}.\)

a) Diện tích phần còn lại của khu vườn là: \(a\left( {a - 8} \right) - {b^2}{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

b) Diện tích phần còn lại của khu vườn khi \(a = 50{\rm{ m}}{\rm{, }}b = 10{\rm{ m}}\) là: \(50\left( {50 - 8} \right) - {10^2} = 2{\rm{ }}000{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).

a) \(A\left( x \right) = \frac{3}{4}{x^3} - 1 + \frac{3}{5}x + 4{x^2} + \frac{5}{4}{x^3} - \frac{8}{5}x + 4 + 7{x^2}\)

             \( = \left( {\frac{3}{4} + \frac{5}{4}} \right){x^3} + \left( {4 + 7} \right){x^2} + \left( {\frac{3}{5} - \frac{8}{5}} \right)x - 1 + 4\)

             \( = 2{x^3} + 11{x^2} - x + 3\).

b) Bậc của đa thức \(A\left( x \right)\) là 3.

Hệ số cao nhất của đa thức \(A\left( x \right)\) là 2.

c) \(B\left( x \right) = \left( {{x^2} + 1} \right)\left( {2x + 11} \right) - 5x - 8\)

              0\( = 2{x^3} + 11{x^2} + 2x + 11 - 5x - 8\)

              \( = 2{x^3} + 11{x^2} - 3x + 3\)

Ta có \(B\left( x \right) - C\left( x \right) = A\left( x \right)\).

Suy ra \(C\left( x \right) = B\left( x \right) - A\left( x \right)\)

                    \( = 2{x^3} + 11{x^2} - 3x + 3 - \left( {2{x^3} + 11{x^2} - x + 3} \right)\)

                    \( = 2{x^3} + 11{x^2} - 3x + 3 - 2{x^3} - 11{x^2} + x - 3\)

                    \( = - 2x\).

d) Để tìm nghiệm của đa thức \(C\left( x \right)\), ta cho \(C\left( x \right) = 0\)

Do đó \( - 2x = 0\)

Suy ra \(x = 0\).

Vậy nghiệm của đa thức \(C\left( x \right)\) là \(x = 0\).

5.1.

Trong tam giác \[ABC\] vuông tại \[A\] có \[AB = AC\] nên \[\Delta ABC\] vuông cân tại \[A.\]

Suy ra \[\widehat {ABC} = \widehat {ACB} = 45^\circ \].

Xét \[\Delta ADC\] có \[AC = DC\] nên \[\Delta ADC\] cân tại \[C\].

Suy ra \[\widehat {CDA} = \widehat {CAD} = x\].

Ta lại có \[\widehat {BCA}\] là góc ngoài của \[\Delta ADC\].

Suy ra \[\widehat {BCA} = \widehat {CDA} + \widehat {CAB} = x + x = 2x\].

Do đó, \[2x = 45^\circ \] nên \[x = 22,5^\circ \].

5.2.

a) Xét \(\Delta ACE\) và \(\Delta KCE\) có:

\(\widehat {CAE} = \widehat {CKE} = 90^\circ \);

\(EC\) là cạnh chung;

\(\widehat {ACE} = \widehat {KCE}\) (do \(CE\) là tia phân giác của \(\widehat {ACB}\)).

Do đó \(\Delta ACE = \Delta KCE\) (cạnh huyền – góc nhọn).

Suy ra \(EA = EK\) và \(CA = CK\) (các cặp cạnh tương ứng).

Do đó \(CE\) là đường trung trực của đoạn thẳng \(AK\) nên \(CE \bot AK\).

b) Xét \(\Delta ABC\) vuông tại \(A\) có \(\widehat {ABC} + \widehat {ACB} = 90^\circ \)

Suy ra \[\widehat {ABC} = 90^\circ - \widehat {ACB} = 30^\circ \].

Lại có \(CE\) là tia phân giác của \(\widehat {ACB}\) nên \(\widehat {ACE} = \widehat {KCE} = 30^\circ \).

\(\Delta BCE\) có \(\widehat {ABC} = \widehat {ECB} = 30^\circ \) nên là tam giác cân tại \(E\).

\(\Delta BCE\) cân tại \(E\) có \(EK\) là đường cao nên đồng thời là đường trung tuyến, hay \(K\) là trung điểm của \(BC\).

Do đó \(BK = KC\) và \(BC = 2KC\)

Mà \(AC = KC\) (câu a) nên \(BC = 2AC\).

Xét \(\Delta BKE\) vuông tại \(K\) có \(BE\) là cạnh huyền nên là cạnh lớn nhất của tam giác

Do đó \(BE > BK\) mà \(BK = KC = AC\) nên \(BE > AC\).

c) Giả sử hai đường thẳng \(BD\) và \(AC\) cắt nhau tại \(I\).

Xét \(\Delta IBC\) có hai đường cao \(BA,CD\) cắt nhau tại \(E\) nên \(E\) là trực tâm của tam giác.

Suy ra \(IE \bot BC\).

Mà \(EK \bot BC\) nên ba điểm \(I,E,K\) thẳng hàng.

Vậy ba đường thẳng \(AC,EK,BD\) đồng quy.